Wprowadzenie do elektroniki/Definicje i wzory
Definicje i wzory
[edytuj]Podstawy budowy atomu
[edytuj]| Atom jest najmniejszą częścią pierwiastka, zdolną do samodzielnego istnienia, która zachowuje wszystkie cechy tego pierwiastka |
Atom jest zbudowany z dodatnio naładowanego jądra, zawierającego dodatnio naładowane protony i obojętne elektrycznie neutrony i sfery elektronowej, gdzie ujemnie naładowane elektrony krążą po powłokach wokół jądra. Maksymalną ilość elektronów na danej powłoce możemy obliczyć ze wzoru (gdzie n to numer powłoki). Liczba elektronów i protonów w atomie jest sobie równa, przez co cały atom jest elektrycznie obojętny. Najbardziej oddalona powłokę od jądra nazywamy powłoką walencyjną, a elektrony po niej krążące - walencyjnymi. Elektrony te charakteryzują się dużą energią i słabym związaniem z jądrem, przez co łatwo je "wybić" z powłoki dostarczając energię np. w postaci ciepła lub światła. Elektrony "uwolnione" z atomu nazywamy elektronami swobodnymi. Swobodne elektrony tworzą w przewodnikach tzw. chmurę elektronową, gdzie poruszają się chaotycznie. Pod wpływem pola elektrycznego elektrony zaczynają poruszać się w sposób uporządkowany.
| Uporządkowany ruch elektronów nazywamy prądem elektrycznym |
Pole elektryczne
[edytuj]Natężenie pola elektrycznego
[edytuj]Natężenie pola elektrycznego możemy sprawdzić, umieszczając ładunek próbny q w badanym polu elektrycznym a następnie mierząc siłę działającą na ten ładunek. Aby wynik pomiaru był miarodajny należy otrzymaną wartość podzielić przez wartość ładunku próbnego.
Jednostką natężenia pola jest
Pole magnetyczne
[edytuj]Indukcja magnetyczna i strumień magnetyczny
[edytuj]Indukcją magnetyczną nazywamy stosunek siły F działającej na dodatni ładunek q, poruszający się prostopadle do linii pola magnetycznego do iloczynu wartości tego ładunku i jego szybkości v
Jednostką indukcji jest
Strumieniem magnetycznym przenikającym ciało nazywamy iloczyn indukcji B oraz pola powierzchni ciała S, przez które przenika strumień.
jednostka-weber[Wb]=[Tm²]
Prąd sinusoidalny
[edytuj]Powstawanie prądu sinusoidalnego
[edytuj]Najprostsza prądnica
Prąd sinusoidalny popłynie przez ramkę poprzez jej obrót w jednorodnym polu magnetycznym.Zachodzą wówczas ciekawe zależności:
α=0° Ψ=max I=0
Ramka jest ułożona prostopadle do linii strumienia magnetycznego. Strumień jest wówczas największy, lecz prąd, wbrew pozorom, nie płynie.
α=90° Ψ=0 I=max
Ramka jest ułożona równolegle do linii pola magnetycznego. Strumień jest zerowy, a prąd - maksymalny.
Później sytuacja jest analogiczna:
α=180° Ψ=-max I=0
α=270° Ψ=0 I=-max
Sytuacja ta wynika z tego, iż siła elektromotoryczna indukowana w ramce wyrażana jest zależnością
Tłumacząc na z matematycznego na nasze. Wielkość indukowanego napięcia zależy nie od wielkości strumienia przenikającego ramkę, ale od szybkości jego zmian.
Jeszcze inaczej:
Jeśli wielkość strumienia przenikającego ramkę opiszemy wzorem
to pochodna tego będzie siłą elektromotoryczną i będzie funkcją cosinus. po zróżniczkowaniu mamy
Prąd sinusoidalny - opis matematyczny
[edytuj]Przebieg sinusoidalny możemy przedstawić przy pomocy wirującego wektora o stałej długości oraz stałej prędkości kątowej. sytuację taką przedstawiam na rysunku poniżej
zakładając iż prędkość kątowa wynosi ω wówczas kąt φ możemy wyliczyć z zależności
przebieg sinusoidalny prądu możemy opisać równaniem:
- faza początkowa przebiegu.
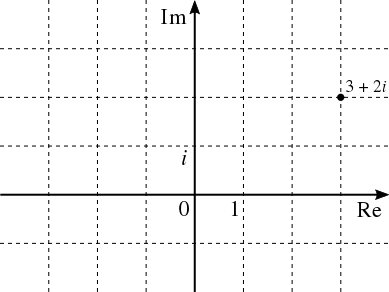
Obliczenia wykonywane w takiej postaci są powiedzmy niewygodne, a bardziej skomplikowane układy stawały by się wręcz udręką. Z pomocą przychodzą nam liczby zespolone. Liczba zespolona pozwala nam zapisać właśnie taki wirujący wektor w postaci amplituda i faza początkowa. Ponieważ dodawanie przebiegów sinusoidalnych o tych samych częstotliwościach nie wpływa na zmianę tych częstotliwości - zmianie ulega tylko amplituda i faza początkowa. Do opisu przebiegów sinusoidalnych wygodnie jest użyć liczb zespolonych. [1] Jest to pewien sposób przedstawienia wektora przy czym oś X jest nazwana częścią rzeczywistą liczby zespolonej a oś Y jest nazywana częścią urojoną liczby zespolonej.
Do stosowania liczb zespolonych w elektrotechnice przyczyniają się właściwości tychże liczb.
| W wyniku mnożenia dwóch liczb zespolonych otrzymujemy liczbę, której długość jest równa iloczynowi długości wektorów, a kąt jest równy sumie kątów. |
| Dodawanie liczb zespolonych odbywa się tak jak dla zwykłych wektorów. dodajemy części rzeczywiste i urojone do siebie |
Z prawa Ohma U=I*Z oczekujemy, że wartość napięcia będzie iloczynem wartości prądu i impedancji a faza początkowa napięcia będzie równa fazie początkowej prądu przesuniętej o kąt impedancji:) To właśnie dają nam liczby zespolone.
Przykład.
[edytuj]W układzie szeregowym rezystor kondensator R=1.5Ω , Xc=2Ω płynie prąd . policzyć napięcie zasilające.
Impedancja zespolona Ponieważ napięcie na kondensatorze opóźnia się za prądem o 90° składnik reaktancji kondensatora mnożymy przez -j(mnożenie przez j w dziedzinie liczb zespolonych powoduje przesunięcie wektora o 90°)
Długość wektora wyliczamy z twierdzenia Pitagorasa.
Kąt początkowy wyliczamy z zależności °
Co pozwala nam zapisać wartość napięcia zasilającego układ w postaci



![{\displaystyle [{\frac {V}{m}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47efbd671a3ae04ef6649f1e0443fa2403093d38)

![{\displaystyle [T]Tesla\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f4b171c773413d593a2e15d6500ff8d06c30974)