GNU Octave/Numeryczne rozwiązywanie równań różniczkowych

Numeryczne rozwiązywanie równań różniczkowych zwyczajnych pierwszego rzędu

Rozwiązanie równania $y'=-ax,\,y(0)=1,\,a=0.1$, na przedziale [0,10]

Za pomocą funkcji lsode rozwiązać równania różniczkowe, tj. znaleźć funkcję y=y(x), taką, że:

1. ${\begin{cases}y'=-ay,x\in [0,1],a=\pm {}0.1,\pm {}1,\pm {}100\\y(0)=1\end{cases}}$
2. ${\begin{cases}y'=y^{2},x\in [0,3]\\y(0)=1\end{cases}}$
3. ${\begin{cases}y'=y\cdot {}x\sin(ax),x\in [0,20]\\y(0)=1\end{cases}}$

Rozwiązania powyższych równań można wyznaczyć symbolicznie, są to:

1. $y=e^{ax}\,$
2. $y={\frac {1}{1-x}}\,$
3. $y=e^{(\sin(ax)-ax\cos(ax))/a^{2}}$, gdzie $a=100$

Rozwiązanie równania $y'=y^{2},\,y(0)=1$, na przedziale [0, 0.99]

Zdefiniujmy funkcje, które występują w równaniach:

 function y=linfun(x)
    global a;
    y=a.*x;
 endfunction;

 function y=kwadfun(x)
    y=x.*x;
 endfunction;

 function y=mixfun(x,t)
    y=x.*t.*sin(t*100);
 endfunction;

Rozwiązanie równania $y'=y\cdot {}x\sin(x)$ na przedziale [0,20]. Dosalismy fale o bardzo dużym nachyleniu i coraz większych amplitudach.

Rozwiążmy pierwsze równanie: Zadajemy wartość dla współczynnika a:

 global a;
 a=0.1;
 %Zadajemy przedział, na którym będziemy rozwiązywać równanie:
  t=[0:0.01:1];
 %Zadajemy warunek brzegowy w pierwszym punkcie czasowym <tt>t(1)</tt>, czyli w <tt>t=0</tt>:
  x0=1; 
 %Rozwiązujemy równanie:
  Z=lsode("linfun", x0, t);
 %Rysujemy rozwiązanie:
  plot(t,Z,"-r")

Podobnie rozwiązujemy drugie równanie:

 t=[0:0.01:0.99];
 x0=1;
 Z=lsode("kwadfun", x0, t);

Funkcja $1/(1-x)$ wybucha w $x=1$.

Rozwiązujemy trzecie równanie:

 t=[0:0.01:20];
 x0=1;
 Z=lsode("mixfun", x0, t);
 axis([0, 20, 0, 2]);
 plot(t, Z, "-r");

Numeryczne rozwiązywanie równań różniczkowych zwyczajnych wyższych rzędów

Rozwiązać równanie różniczkowe 2. rzędu:

${\begin{cases}x''=f(x)=-x\\x(0)=0\\x'(0)=1\\\end{cases}}$

Równanie to można scałkować symbolicznie, a jego rozwiązaniem jest $x(t)=sin(t)$.

Aby rozwiązać równanie numerycznie, przekształcimy je do równania pierwszego rzędu, w którym zmienna jest wektorem i rozwiążemy za pomocą funkcji lsode. Przekształcone równanie dla zmiennej ${\overline {x}}=[x_{1},x_{2}]=[x(t),x'(t)]$ ma postać:

${\begin{cases}x_{1}'=x_{2}\\x_{2}'=f(x_{1})=-x_{1}\\x_{1}(0)=0\\x_{2}(0)=1\end{cases}}$

Wykres rozwiązania $[x,x']$ równania $x''=-x$ z warunkami początkowymi $x(0)=0$, $x'(0)=1$

Zdefiniujmy funkcję:

 function y=ujfun(x)
    y(1)= x(2);
    y(2)=-x(1);
 endfunction;
%Rozwiązujemy równanie <math>\overline{x}'=\texttt{ujfun}(\overline{x})</math>: 
 x0=[1;0];
 t=[0:0.005:100];
 Z=lsode("ujfun", x0, t);

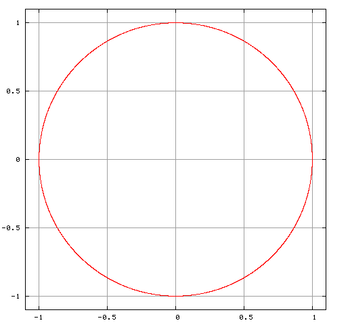
Zauważmy, że warunek początkowy jest pionowym 2-elementowym pionowym wektorem $[1;0]$. Narysujmy wykres $[x_{1},x_{2}]$:

 plot(Z(:,2),Z(:,1),"-r");

Wynikiem jest okrąg, czyli zbiór $\{\,[\sin(t),\cos(t)]\,:t\in [0,2\pi ]\}$, co zgadza się z rozwiązaniem teoretycznym.

Numeryczne rozwiązywanie równań różniczkowych zwyczajnych z "odwróconym" warunkiem początkowym

Rozpatrzmy zagadnienie Cauchy'ego dla równania różniczkowego:

${\begin{cases}x'=f(x,t),x\in [0,1]\\x(0)=s\end{cases}}$

Równanie jest sparametryzowane parametrem $s\in [0,1]$ i dla zadanej funkcji $f$. Oznaczmy $y_{s}(t)$ rozwiązanie równania dla ustalonego $s$. Dla jakiego $s$ dostaniemy $y_{s}(1)={\frac {1}{2}}$? Innymi słowy, jeśli oznaczymy $F(s)=y_{s}(1)$ należy rozwiązać równanie:

$F(s)={\frac {1}{2}}$

Jak wygląda potok $y_{s}(t)$ i wykres $F(s)$? Rozważmy funkcję $f(y,t)=sin(y^{2}+1)*y*(1-y)$.

Wykres potoku dla zagadnienia Cauchy'ego dla równania różniczkowego $x'=\sin(x^{2}+1)x(1-x)$ z warunkiem początkowym $x(0)=s$ na przedziale $t\in [0,1]$ parametryzowanego parametrem $s\in [0,1]$. Linia, która "kończy" się w $(1,0.5)$ zaczyna się w przybliżeniu w $(0,0.3)$.

Najpierw rozwiążemy szukane równanie. Zdefiniujmy funkcję występującą w równaniu:

 function y=dfun(x)
    y=sin(x.^2.+1).*x.*(1.0.-x);
 endfunction;

%Rozwiązujemy równanie dla zadanego parametru <math>s</math> na przedziale <math>[0,1]</math>:
 function y=dfunSolveODE(s)
    t=[0:0.01:1];
    y=lsode("dfun", s, t);
 endfunction;

%Rysujemy wykres funkcji <math>F(s)=y_s(1)=dfunsolve(s)</math>:
 s=[0:0.01:1];
 y=dfunSolveODE(s);
 plot(s,y);

%Rozwiązujemy równanie <math>F(s)-\frac{1}{2}=0</math>. Zdefiniujmy funkcję:
 function y=dfunMinusPol(s)
    z=dfunSolveODE(s);
    y=z(length(z))-0.5;
 endfunction;

% i znajdźmy jej [[w:miejsce zerowe|miejsce zerowe]]:
 fsolve("dfunMinusPol",0.3)
 ans = 0.28628

Numeryczne rozwiązywanie równań różniczkowych zwyczajnych z warunkami brzegowymi

Znaleźć funkcję $u=u(t)$ spełniającą równanie różniczkowe z warunkami brzegowymi:

${\begin{cases}u''+u^{2}=f(t)\\u(0)=0,u(1)=0\end{cases}}$

Dla funkcji $f(t)=sin(t)$.

Aby rozwiązać to zagadnienie trzeba znaleźć taki parametr $s_{0}$, żeby rozwiązanie zagadnienia

${\begin{cases}u''+u^{2}=f(t)\\u(0)=0,u'(0)=s_{0}\end{cases}}$

spełniało zadany warunek brzegowy w drugim końcu przedziału, tj. $u(1)=0$. Można to zrobić metodą z "odwróconym" warunkiem początkowym, opisaną wcześniej. Przekształćmy zagadnienie na równanie pierwszego rzędu zmiennej $[x_{1},x_{2}]=[u(t),u'(t)]$:

${\begin{cases}x_{1}'=x_{2}\\x_{2}'=-x_{1}^{2}+f(t)\\x_{1}(0)=0\\x_{2}(0)=s_{0}\end{cases}}$

Potok fazowy dla równania $u''+u^{2}=sin(t)$ z warunkami początkowymi $u(0)=0$ i $u'(0)=s$ dla parametrów $s\in [-1,1]$.

Zdefiniujmy funkcje występujące w równaniu:

 function y=d1fun(x,t)
    y(1)=x(2);
    y(2)=-x(1)^2+d1funF(t);
 endfunction;
 function y=d1funF(t)
    y=sin(t);
 endfunction;

%Zdefiniujmy funkcję, która rozwiązuje równanie dla zadanego parametru:
 function y=d1funSolveODE(s)
    t=[0:0.01:1];
    x0=[0;s];
    y=lsode("d1fun", x0, t);
 endfunction;

Narysujmy potok fazowy dla tego równania dla wartości $s_{0}\in [-1,1]$. (Dokładniej: Funkcja d1funSolveODE działa poprawnie dla pojedynczej wartości parametru s. Aby wywołać rysowanie tak, jak poniżej, trzeba lekko zmienić jej treść).

 s=[-1:0.03:1];
 y=d1funSolveODE(s);
 plot(t,y);

Widzimy, że szukana krzywa przechodząca przez punkty $(0,0)$ oraz $(1,0)$ ma w $t=0$ nachylenie bliskie 0.

Rozwiązanie równania $u''+u^{2}=sin(t)$ z warunkami brzegowymi $u(0)=0$ i $u(1)=0$.

Wyznaczymy teraz tę wartość dokładnie. Zdefiniujmy funkcję $u_{s}(1)$

 function y=d1funFunIn1(s)
    z=d1funSolveODE(s);
    w=z(:,1);
    y=w(length(w));
 endfunction;
% i rozwiążmy równanie:
 s0=fsolve("d1funFunIn1", 0)

%Dostajemy wartość: 
 s0 = -0.15769

%Rysujemy rozwiązanie:
 z=d1funSolveODE(s0);
 plot(t, z(:,1);

Rozwiązanie rzeczywiście przechodzi przez punkty $(0,0)$ i $(1,0)$.