Wstęp do fizyki jądra atomowego/Nukleony a budowa jądra atomowego

Nukleony a budowa jądra atomowego

---

Licencja

Autor: Mirosław Makowiecki Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność.

---

---

Etap współczesny

Według stanu obecnego fizykę dzielimy na działy: jądra atomowego, cząstek elementarnych i kosmosu (chodzi tutaj o strukturę i teorię powstania wszechświata). W wyniku rozwoju techniki eksperymentalnej, tzn. akceleratorów, detektorów, elektroniki i komputerów, badano własności jąder atomowych i strukturę materii w wysokoenergetycznych wiązkach akceleratorowych p, e^- i e⁺ i innych cząstek, i w promieniowaniu kosmicznym. Nuklidami nazywamy jądra o ściśle określonej liczbie atomowej Z i masowej A. Odkryto ponad 3000 nuklidów (Z=od 1 do 118), 150 obiektów (cząstek) początkowo traktowanych jako cząstki elementarne. W 1964 r. Badano strukturę hadronów. M. Gell-Mann i G. Zweig postulowali, że te właśnie cząstki są złożone z trzech kwarków i jest to model kwarkowy hadronów. W latach siedemdziesiątych trzy kwarki już nie wystarczają do opisu nowych hadronów, rozwija się teoria oddziaływań silnych QCD. Odkryto sześć leptonów i sześć kwarków wraz z ich antycząstkami, które różnią się zapachem i kolorem, w sumie tworzą trzy generacje. Cząstki złożone z trzech kwarków są bezbarwne. Każdy kwark występuje w trzech kolorach (w stanach kolorowych), charakteryzujących się elektrycznym ładunkiem ujemnym (-1/3)e lub ładunkiem dodatnim (2/3)e. Kwarki oddziałują ze sobą przy pomocy gluonów, które są bozonami o masie spoczynkowej równej zero i ładunku zerowym, ale mają ładunek kolorowy, ale występujących w ośmiu kolorach. Kwarki i gluony są uwięzione w hadronach, z których na przykład proton składa się z trzech kwarków (u,u,d): (2/3+2/3-1/3)e=e. Podobnie neutron składa z trzech kwarków (ddu): (-1/3-1/3+2/3)e=0. Mezony natomiast składają się z dwóch kwarków (kwark + antykwark).

Model standardowy materii

Cząstki fundamentalne składają się z sześciu leptonów i sześciu kwarków wraz z ich antycząstkami. Kwantową teorię pola elektromagnetycznego oraz słabego możemy połączyć w oddziaływanie elektrosłabe, model oddziaływania silnego i elektrosłabego możemy połączyć w model standardowy.

Podstawowe cząstki elementarne w fizyce cząstek elementarnych
Cząstka	Nazwa cząstki	Masa (GeV/c2)	Ładunek
$\nu _{e}\;$	Neutrino elektronowe	$<7\cdot 10^{-9}\;$	0
e	Elektron	0,0005111	-1
$\nu _{\mu }\;$	Neutrino mionowe	<0,0003	0
$\mu ^{-}\;$	Mion	0,106	-1
$\nu _{\tau }\;$	Neutrino taonowe	<0.03	0
$\tau ^{-}\;$	Taon	1.7771	-1

W poniższej tabelce pokazaliśmy powierzchowne informacje o kwarkach, których jest sześć i których ładunki są ułamkowe, tzn. ich ładunki są oznaczane przez (+2/3)e i przez (-1/3)e.

Kwarki w modelu standardowym
Cząstka	Nazwa cząstki	Masa (GeV/c2)	Ładunek
μ	górny	0,005	+2/3
d	dolny	0,01	-1/3
c	powabny	1.5	+2/3
s	dziwny	0,2	-1/3
t	szczytowy, wysoki, prawdziwy	180	+2/3
b	piękny, niski	4,7	-1/3

Jeśli traktować, że 1 (jedynka) to jest 10^-18m, to elektron ma wielkość mniejszą od jedynki, kwark o rozmiarach 10^-18m ma rząd równy jedynce, proton ma wielkość równą 1000 (on ma rozmiary w metrach 10^-15m), jądro ma wielkość 10000 o rozmiarach 10^-14m, a atom ma wielkość 100000000 o rozmiarach 10^-10m. Atomy, jądra i nukleony nie są kulami to jest tylko rząd wielkości. Elektron ma rozmiary bardzo małe i dlatego nie mówi się o rozmiarach elektronów.

Jądra atomowe

Jądra składają się z protonów i neutronów, gdzie liczba protonów wynosi Z (liczba porządkowa atomu), liczba neutronów N, a liczbę masową oznaczamy przez A, która jest równa licznie neutronów N i liczbie atomowej Z:

$A=N+Z\;$

(1.1)

Ogólnie symbol pierwiastka oznaczamy jak poniżej:

${}_{Z}^{A}{\hbox{X}}_{N}\;$

(1.2)

Przykładem jąder atomowych są:

• ${}_{1}^{1}H\;$, ${}_{1}^{2}H$, ${}_{1}^{3}H\;$, ${}_{2}^{4}He\;$, ${}_{82}^{208}Pb\;$, ${}_{92}^{238}U\;$.

Jądra atomowe dzielimy ze względu na liczbę atomową (liczbę protonów) Z, masową A i liczbę neutronów w jądrze N.

• Izotopy , których liczba atomowa Z jest wielkością stałą, np. ${}_{1}^{1}H\;$, ${}_{1}^{2}H\;$ i ${}_{1}^{3}H\;$.
• Izotony , których liczba neutronów N w jądrze jest wielkością stałą, np. ${}_{1}^{3}H\;$ i ${}_{2}^{4}He\;$.
• Izobary , których liczba protonów i neutronów razem wziętych jest wielkością stałą, ${}_{1}^{3}H\;$ i ${}_{2}^{3}He\;$.

Jądra dzielimy też ze względu na liczbę nukleonów w jądrze na:

• Jądra parzyste , w których A jest parzyste, ale Z i N też są liczbami parzystymi.
• Jądra nieparzyste , w których liczba masowa A jest liczbą nieparzystą.

Ze względu na stabilność dzielimy je na:

• jądra stabilne , których znamy 274 w tym 215 jąder typu p-p (parzysto-parzyste) i 4 typu n-n (nieparzysto-nieparzyste).
• jądra niestabilne , są to jądra promieniotwórcze ze względu na rozpad α,β, sf i emisję nukleonów.

Nuklid

Jest to atom o określonej liczbie atomowej (A,Z). Przykładem są nuklidy pierwiastka wodoru $H,{\mbox{ czyli }}{}_{1}^{1}H,{}_{1}^{2}H,{}_{1}^{3}H.\;$.

Siły jądrowe

(Rys. 1.1) Charakter sił jądrowych

Nukleony w jądrze są związane siłami jądrowymi, które są wynikiem sił oddziaływania silnego, mającego krótki zasięg $(\leq 2\cdot 10^{-15}m)\;$. Te siły nie zależą od rodzaju nukleonów, z którymi mamy doczynienia. Potencjał omawianego tutaj oddziaływania zależy od współrzędnej radialnej, jeśli przedstawić oddziaływanie silne w układzie współrzędnych kulistym V=V(r). Stała sprzężenia oddziaływania silnego wynosi $\alpha _{s}\simeq 1\;$. Oddziaływania te ulegają wysycaniu. Przykłady stałej sprzężenia dla innych oddziaływań są:

• pole grawitacyjne $\alpha \simeq 5.6\cdot 10^{-39}\;$,
• oddziaływanie słabe $\alpha _{sl}\simeq 1\cdot 10^{-5}\;$,
• oddziaływanie elektromagnetyczne $\alpha ={{1} \over {137}}\;$.

Masa i energia wiązania jąder atomowych i nuklidów

Masę atomową nuklidów wyrażamy w jednostkach masy atomowej, która według definicji jest równa 1/12 masy atomu węgla ${}_{6}^{12}C\;$, co schematycznie możemy przedstawić:

$1u={{1} \over {12}}M({}_{6}^{12}C)=1,66\cdot 10^{-24}g=931,5016(3)MeV/c^{2}\;$

(1.3)

Masę protonu, neutronu, a także elektronów piszemy w jednostkach masy atomowej, które to przeliczamy na energię (będąca równoważna z masą):

• $m_{p}=1,007276470(11)u=938,2796(27)MeV/c^{2}\;$
• $m_{n}=1,008665012(37)u=939,5731(27)MeV\;$
• $m_{e}=5,4858026(21)\cdot 10^{-4}u=0,5110034(14)MeV/C^{2}\;$

Różnica masy neutrony i protonu jest równa dwa i pół masy elektronu, tzn.:

$m_{n}-m_{p}\simeq 1.29MeV\simeq 2.5m_{e}\;$

(1.4)

Neutron swobodny jest cząstką nietrwałą o czasie połowicznego zaniku równym T_1/2=10,6m i on rozpada się na proton, elektron i antyneutrino elektronowe wedle:

$n\rightarrow p+e^{-}+{\tilde {\nu }}_{e}({\mbox{rozpad }}\beta ^{-})\;$

(1.5)

Budowa jądra atomowego i jego energia wiązania

Znając masy protonu, neutronu, elektronu i atomów można by oczekiwać, że po zsumowaniu mas Z protonów, N neutronów i Z elektronów ich suma będzie równa masie atomu. Rzeczywistość jest jednak inna, masa atomu jądra atomowego jest mniejsza niż oczekiwana. Niedobór masy można napisać według jego definicji:

$Zm_{p}+(A-Z)m_{n}+Zm_{e}-M_{a}=\Delta M\;$

(1.6)

Przy łączeniu cząstek wchodzących w skład atomu wydziela się pewna energia, którą można opisać z równoważności masy i energii:

$E_{W}=\Delta Mc^{2}\;$

(1.7)

Do rozkładu jądra na składniki należy dostarczyć jądru energię równą (1.7), którą tutaj oznaczymy przez B(A,Z).

Każdy atom składa się z jądra i elektronów, a jądro atomowe składa się z neutronów i protonów. Masa jądra nie jest sumą mas jego składników, tzn. protonów i neutronów. Energia wiązania jądra atomowego, w takim przypadku nazywamy różnicę sumy mas poszczególnych składników wchodzących w skład jądra atomowego i masy jądra, jest ona równa:

$\Delta M(A,Z)=Zm_{p}+(A-Z)m_{n}-M_{a}\;$

(1.8)

Masa elektronu jest bardzo mała, można więc masę protonu zastąpić przez masę atomu wodoru, wtedy wzór (1.6) zapisujemy:

$\Delta M(A,Z)=Zm_{H}+(A-Z)m_{n}-M_{a}\;$

(1.9)

• gdzie M_a jest masą jądra atomowego, już po połączeniu nukleonów w skład jądra atomowego.

Znając defekt masy jądra atomowego w unitach możemy policzyć masę jądra przedstawionych w MeV:

$E_{W}=B(A,Z)=\Delta M\cdot 931{{MeV} \over {u}}\;$

(1.10)

Energia wiązania jądra w przypadku atomu helu wynosi: B(A,Z)=28,39 MeV. Wyzwalana jest w trakcie powstawania jądra atomowego helu z czterech nukleonów (dwa neutrony i dwa protony). Można policzyć, że podczas powstawania 1 kg helu zostaje wyzwolona energia równa spaleniu 25 000 ton węgla.

Znając energię wiązania B(A,Z) (1.10) możemy policzyć średnią energię przypadająca na jedno wiązanie, która jest ilorazem energii wiązania przez liczbę masową A, i wynosi ona:

${\mathcal {E}}(A,Z)={{B(A,Z)} \over {A}}\;$

(1.11)

Im większa jest energia średnia wiązania atomu, tym bardziej jądro jest trwalsze, tzn. należy dostarczyć więcej energii by rozłożyć atom na składniki.

Masa jądra atomowego

Masę jądra atomowego możemy wyliczyć znając masę neutronu i protonu, a także energię wiązania nukleonów jądra atomowego na podstawie wzoru (1.9):

$M(A,Z)=Zm_{p}+(A-Z)m_{n}-B(A,Z)\;$

(1.12)

W tablicach są podane masy nuklidów (M(A,Z) (lub energie wiązania jądra z elektronami), które możemy wyrazić:

$M(A,Z)=M_{j}(A,Z)+Zm_{e}-B(elektr.)\;$

(1.13)

Energia wiązania jądra z elektronami wyrażamy:

$B(elektr.)\simeq (0,01Z)^{2,5}MeV\;$

(1.14)

Energia wiązania dla jądra elektronu z jądrem wodoru wyrażamy wzorem $B(elektr.)=B({}_{1}^{1}H)=({}_{1}^{1}H)=({}_{1}^{1}H)=13,6eV\;$, a według wzoru (1.14) wynosi $B({}_{1}^{1}H)=({}_{1}^{1}H)\simeq 10eV\;$. Ponieważ masa jądra atomu praktycznie się nie różni od masy całego atomu (jądra z krążącymi wokół elektronami), zatem masę protonu możemy zastąpić przez masę wodoru ${}_{1}^{1}{\hbox{H}}\;$, co schematycznie piszemy:

$M(A,Z)=ZM({}_{1}^{1}H)+(A-Z)m_{n}-B(A,Z)\;$

(1.15)

• gdzie B(A,Z) jest to energia wiązania nuklidów.

Dla jąder izobarycznych jądrami najbardziej stabilnymi są te o największej energii wiązania i są one stabilne ze względu na rozpady β, podczas gdy mogą one być niestabilne ze względu na rozpad α, sf.

Odchylenie masy (mass excess)

Odchyleniem masy nazywamy różnicę masy jądra atomowego (1.12) w unitach i liczby masowej pomnożonej przez unity:

$ME(A,Z)=\left({{M(A,Z)} \over {u}}-A\right)u\;$

(1.16)

Co wzór (1.16) możemy wyrazić nie tylko w w unitach, czyli w jednostkach masy atomowej, ale też ją zwykle wyrażamy w jednostkach energii MeV korzystając z przelicznika (1.10). Energia wiązania B(A,Z) decyduje o stabilności w zależności na naturalne rozpady β α, sf, itp. W zbiorze jąder izobarycznych o danym A jądra o największej energii wiązania są stabilne ze względu na rozpady β, te jądra mogą być również ze względu na rozpad α, sf.

Średnia energia wiązania nukleonów

(Rys. 1.2) Średnia energia wiązania

Jak można zauważyć według rysunku obok, że średnia energia wiązania jąder atomowych ${\mathcal {E}}\;$ (1.5) rośnie w obszarze jąder lekkich wykazując lokalne maksima przy A=4,8,12,16,....

• W pobliżu A=60 uzyskuje płaskie maksimum E^max=8.8MeV.
• Powoli maleje dla dużych A>60 osiągając w końcu energię E^ciężkie=7.6MeV
• Wykazuje lokalne wzrosty dla liczby Z lub N=2,8,20,(28),50,(64),82,126, które to nazywamy liczbami magicznymi.

Jadrami podwójnie magicznymi są to jądra opisane jako:

• ${}_{2}^{4}He_{2}\;$, ${}_{8}^{16}O_{8}\;$, ${}_{20}^{40}Ca_{20}\;$, ${}_{50}^{132}Sn_{82}\;$,  ${}_{(64)}^{146}Gd_{82}\;$, ${}_{82}^{208}Pb_{126}\;$.

Wysycanie sił jądrowych powodowane jest przez istnienie oddziaływań n-n silnie odpychającego rdzenia, które nie pozwalają zbliżyć nukleonom na dowolnie bliskie odległości, co jest powodem ograniczania liczbę sąsiadów danego nukleonu. Powolny spadek B/A dla A>60 występuje w wyniku wzrostu odpychania kulombowskiego protonów, natomiast spadek B/A dla jąder lekkich tłumaczy się rosnącą rolę efektów powierzchniowych, które są istotne dla małych jąder atomowych.

Materia jądrowa (rozkłady gęstości ładunku i masy atomowej)

Jądra są obiektami fizycznymi związane ze sobą siłami jądrowymi o skończonym zasięgu, które są niezależne od rodzaju nukleonu. Można więc przypuszczać, że jądra atomowe są układami o skończonym zasięgu, a jego brzeg jest niezbyt rozmyty. Energia przypadająca na jednej nukleon w jądrze nie zależy od rodzaju nukleonu i jest niemal stała i wynosi około 8MeV, co świadczy, że siły jądrowe mają właściwość wysycania, czyli każdy przeciętny nukleon jest związany z jego najbliższymi nukleonami. W ciężkich jądrach stosunek B/A jest taki sam w jak cząstce α i wynosi B_α=28,39MeV, w której na każdy nukleon przypadają trzy wiązania, stąd można przepuszczać, że na jeden nukleon przypada najwięcej trzy wiązania jakie tworzy. Można policzyć, że przy wiązaniu 1 kg helu (α) (${}_{2}^{4}He\;$) jest wytwarzana energia równa przy spalaniu 2500 ton węgla. Następstwem wysycania sił jądrowych, w których występuje niezależność ich od rodzaju nukleonu i zakazu Pauliego, jest prawie stała objętość przypadająca na jeden nukleon, co z (1.11) wynika $V\sim A\;$ i zachodzi (1.28) oraz można przypuszczać, że rozkłady materii wewnątrz jądra są takie same.

Wysycanie sił jądrowych w jądrze atomowym pozwala mówić, że w oddziaływaniach n-n o silnie odpychającym rdzeniu, które nie pozwalają się zbliżyć na dowolnie małe odległości nukleonom, ograniczając w ten sposób liczbę najbliższych sąsiadów.

Powolny spadek wartości B/A w ciężkich jądrach dla A>60 tłumaczy się w wyniku wzrostu odpychania kolumbowskiego, natomiast stosunek B/A w jądrach lekkich tłumaczy się jako fakt rosnących efektów powierzchniowych.

Energię separacji (wiązania) nukleonu

Dobrą ilustracją wpływu liczb magicznych nukleonów neutronów i protonów jest tzw. energia separacji, czyli znając masy jądra początkowego ${}_{Z}^{A}X\;$ oraz masę jądra ${}_{Z}^{A-1}X\;$ lub ${}_{Z-1}^{A-1}X\;$ otrzymanego z ${}_{Z}^{A}X\;$ przez odłączenie jednego protonu lub neutronu, wtedy te energie, czyli energię separacji neutronu lub protonu możemy wyrazić przez:

$S_{n}(A,Z)=M(A-1,Z)+M_{n}-M(A,Z)\;$

(1.17)

$S_{p}(A,Z)=M(A-1,Z-1)+M_{p}-M(A,Z)\;$

(1.18)

Energia ta osiąga maksimum dla magicznych liczb dla protonu lub neutronu. Energii separacji protonu lub neutronu wykazuje przy pewnych liczbach atomowych lokalne skoki odpowiadające zamkniętym powłokom nukleonowych, analogicznie do energii jonizacji dla zamkniętych powłok elektronowych. Sugerowanie analogi powłok elektronowych do powłok nukleonowych sugeruje powstawanie liczb magicznych, że umieszczenie nukleonu poza zamkniętą powłoką sugerowałoby zmniejszenie energii separacji, bo słabsze byłyby wiązania pomiędzy nukleonami. Analogicznie do (1.17) i (1.18) energię wiązania neutronu dla jądra atomowego definiujemy przy pomocy energii wiązań jako różnicę energii wiązania dla ściśle określonego Z, ale po dodaniu do jądra jednego neutronu, wtedy z jądra z A powstaje jądro o liczbie masowej A-1, czyli jest to energia potrzebna do wyrwania energii z jądra atomowego wykorzystując (1.15) wychodząc z (1.17) możemy udowodnić, że zachodzi:

$S_{n}(A,Z)=ZM({}_{1}^{1}H)+(A-Z-1)M_{n}-B(A-1,Z)+M_{n}-ZM({}_{1}^{1}H)-(A-Z)M_{n}-B(A,Z)=B(A,Z)+\;$
$-B(A-1,Z)\Rightarrow S_{n}(A,Z)=B(A,Z)-B(A-1,Z)\;$

(1.19)

Energia potrzebna do wyrwania jednego protonu wykorzystując (1.15) wychodząc z (1.17) możemy udowodnić, że zachodzi:

$S_{p}(A,Z)=(Z-1)M({}_{1}^{1}H)+(A-Z)M_{n}-B(A-1,Z-1)+M_{p}-ZM({}_{1}^{1}H)-(A-Z)M_{n}-B(A,Z)=B(A,Z)+\;$
$-B(A-1,Z)\Rightarrow S_{p}(A,Z)=B(A,Z)-B(A-1,Z-1)\;$

(1.20)

Energie separacji neutronu lub protony wykazują silne fluktuacje, które nazywamy efektami powłokowymi, a przykłady tychże energii:

• $S_{n}({}_{1}^{2}{\hbox{H}})=S_{p}({}_{1}^{2}{\hbox{H}})=2,2MeV\;$, $S_{n}({}_{7}^{13}{\hbox{N}})=20,3MeV\;$, $S_{p}({}_{7}^{13}N)=1,9MeV\;$ i $S_{p}({}_{6}^{14}C)=20,8MeV\;$.

Jądra, które są jądrami niestabilnymi ze względu na emisję neutronu, są to jądra, dla których energia separacji neutronu jest mniejsza lub równa zero, czyli $S_{n}\leq 0\;$. Jądra, które są jądrami niestabilnymi ze względu na emisję protonu, są to jądra, dla których energia separacji protonu jest mniejsza lub równa zero, czyli $S_{p}\leq 0\;$.

Doświadczalnie wykazano, że istnieje związek dla energii separacji (dwójkowania, pairing) neutronu (n) lub protonu (p), które to piszemy następująco dla N i Z parzystego:

${\begin{cases}S_{n}(N,Z)>S_{n}(N\pm 1,Z)\\S_{p}(Z,N)>S_{p}(Z\pm 1,N)\end{cases}}\;$

 gdy  

$N\;$ - parzyste

$Z\;$ - parzyste

(1.21)

Nukleony w jądrze atomowym są powiązane w pary (p-p), (n,n), ale nie w parę (n,p), których to moment pędu każdej pary wynosi zero, a więc też spin takiego układu jest równy zero, tzn. $0^{+}\;$.

Energie oddziaływania pairing (parowania nukleonów w jądrze atomowym)

Energia parowania w jądrach atomowym jest to energia tylko oddziaływań silnych i jest to oddziaływanie łączące nukleony w pary pp i nn o przeciwnych spinach, są to krótkozasięgowe oddziaływania wysycające się na najbliższym sąsiedzie tego samego rodzaju, dążą by gęstość jądra atomowego dążyła do izotropowego rozkładu materii. Jest to oddziaływanie resztkowe w jądrach. Energie parowania neutronu i protonu są takie same P_pp≈P_nn, mieszczą się one w zakresie od 2 do 8 MeV, a wzór na energię parowania w zależności od liczby masowej "A" przedstawiamy:

$P={{24} \over {\sqrt {A}}}{\mbox{MeV}}\;$

(1.22)

Jeśli jądro potraktujemy jako pewien układ, to energię wiązania możemy przepisać jako:

$B(Z,N)=\underbrace {B_{c}+B_{sp}(Z,N-1)} _{B(Z,N-1)}+B_{sp}(Z,N)+P_{nn}\;$

(1.23)

Energia parowania nukleonu sparowanego, który definiujemy jako średnią energię dwóch sąsiednich energii separacji względem danego nuklidu, jest:

$B_{sp}(Z,N)]={{1} \over {2}}\left[S_{n}(Z,N-1)+S_{n}(Z,N+1)\right]\;$

(1.24)

Jeśli wykorzystamy wzór na energie separacji neutronu (1.19), ten wzór wykorzystamy do (1.23), stąd wyprowadzamy energię parowania neutronów:

$P_{nn}(Z,N)=B(Z,N)-B(Z,N-1)-B_{sp}(Z,N)=S_{n}(A,Z)-{{1} \over {2}}\left[S_{n}(Z,N-1)+S_{n}(Z,N+1)\right]\;$

(1.25)

Analogicznie do poprzedniego wzoru możemy wykorzystać wzór na energie separacji protonu (1.20) do podobnego wzoru do (1.23) (tylko zmienia się Z zamiast N), wtedy w ten sposób definiujemy energię parowania protonów:

$P_{pp}(Z,N)=S_{p}(Z,N)-{{1} \over {2}}\left[S_{n}(Z-1,N)+S_{n}(Z+1,N)\right]\;$

(1.26)

Energia wiązania każdego nukleonu połączonej w pary, która jest taka sama w przybliżeniu dla neutronu i protonu, wyraża się:

$\Delta _{n}={{P_{nn}} \over {2}}\simeq \Delta _{p}={{P_{pp}} \over {2}}\;$

(1.27)

nazywamy tą energię energią przerwy energetycznej neutronowej Δ_n i protonowej Δ_p, dla którego jak powiedzieliśmy powyżej są w przybliżeniu sobie równe.

Modele jąder atomowych

Model kroplowy

Model kroplowy jest to inaczej zwany modelem Weizsäcke'a i Bethe'go, która mówi:

• gęstość nukleonów w materii jądrowej nie zależy od liczby masowej A, dla którego promień jądra w zależności od liczby masowej i promienia $r_{0}\simeq 1,2\cdot 10^{-13}cm\;$ jest wyrażony:

$R=r_{0}A^{{1} \over {3}}\;$

(1.28)

Gęstość nukleonów możemy przestawić jako ρ=0,17 nukl/fm³, średni promień jądra atomowego jest wyrażony przez $\langle r^{2}\rangle _{nukl}=0,5fm\;$.

• zależność natężenia sił jądrowej jest bardzo podobna do zależności oddziaływania Van der Waalsa działającej w cieczy,
• oddziaływania jądrowe wysycają się tak jak wiązania chemiczne, za wyjątkiem jąder lekkich mamy:

$B_{j}\sim A\Rightarrow {{B_{j}} \over {A}}=\operatorname {const} .\;$

(1.29)

Jądro atomowe opisujemy jako naładowana cząstka o ładunku Q=Ze, która jest nieściśliwą cieczą. Według modelu kroplowego całkowita energia wiązania jest określona:

$B(A,Z)=B_{obj}(A)+B_{pow}(A)+B_{cul}(Z,A)+\underbrace {B_{as}(N,Z)+B_{pairing}} _{\mbox{czlony jądrowe}}\;$

(1.30)

Model kroplowy opisuje średnie właściwości jąder atomowych i nie uwzględnia jego struktury subtelnej. Ten model należy stosować dla jąder o $A\geq 30\;$. Dla jąder stabilnych $A\geq 40\;$ obliczone wartości B(A,Z) zgadzają się z doświadczeniem z błędem ok 2%.

Model kroplowy według Weizsöcke'a i Bethe'go

Energię wiązania jądra atomowego o liczbie atomowej Z i liczbie masowej A przestawiamy:

$B(Z,A)=a_{\nu }A-a_{s}A^{{2} \over {3}}-a_{c}Z^{2}A^{-{{1} \over {3}}}-a_{as}\left(Z-{{A} \over {2}}\right)^{2}A^{-1}\pm \delta \;$

(1.31)

• człon $a_{\nu }A\;$ jest to człon objętościowy pochodzący od przyciągania pochodzącymi od oddziaływania między nukleonami, wartość tej stałej stojąca przy liczbie masowej jest równa a_ν=15,85 MeV, ten współczynnik jest miarą średniego wkładu do energii wiązania (stąd znak minus).

• człon $a_{s}A^{{2} \over {3}}\;$ jest to człon powierzchniowy, nukleony na brzegu mają mniejszą liczbę przyciągających parterów niż nukleony wewnątrz jądra atomowego, liczba nukleonów występujących na powierzchni kuli jest wprost proporcjonalna do pola powierzchni kuli, stała występująca w tym wzorze jest równa a_s=18,34 MeV.

• człon $-a_{c}Z^{2}A^{-{{1} \over {3}}}\;$ jest to człon kulombowski pochodzących od odpychania miedzy nukleonami, wartość stałej występującej przy tym członie jest równa a_c=0,71 MeV.

• człon $-a_{as}\left(Z-{{A} \over {2}}\right)^{2}A^{-1}\;$ jest członem asymetrycznym odzwierciedlających tendencje do ścieżki stabilności N+Z=A=2Z, a stała występująca tutaj jest równa a_as=92,86 MeV.

• człon δ człon charakteryzujący stabilność jąder parzysto-parzystych, mniejszą dla jąder parzysto-nieparzystych i nieparzysto-parzystych i jeszcze mniejszą dla jąder nieparzysto-nieparzystych, ten człon jest wyrażony:
      δ=+Δ dla jąder parzysto-parzystych
      δ=0 dla jądrem A nieparzystych
      δ=-Δ dla jąder nieparzysto-nieparzystych (A parzyste).
  W powyższych rozważaniach przyjęliśmy, że $\Delta =11,46A^{-{{1} \over {2}}}\;$.

Model kroplowy według Myers'a i Świąteckiego

Energię wiązania jądra atomowego w tym modelu analogicznie opisujemy jak we wzorze opisujący model kroplowy Weizsöcke'a i Bethe'go. Jak widzimy, energia wiązania jest pisana wzorem:

$B(A,Z)=15,68A-18,56A^{{2} \over {3}}-0,717Z^{2}A^{-{{1} \over {3}}}\left(1-1,69A^{-{{2} \over {3}}}\right)-28,1(N-Z)^{2}A^{-1}\left(1-1,18A^{-{{1} \over {3}}}\right)\pm \delta {\mbox{ [MeV]}}\;$

(1.32)

• gdzie: $\delta _{p}=11\cdot A^{-{{1} \over {2}}}\;$.

Model kroplowy- dalsze rozważania

Ja widzimy patrząc na wzór (1.31) lub na wzór (1.32), które są energiami wiązania nukleonów w jądrze, wyraża się pewną funkcją kwadratową, którą piszemy dla pewnych wyrazów a, b, c:

$B(Z)=B(Z,A=\operatorname {const} )=aZ^{2}+bZ+c\;$, ale dla $A\;$ parzystego $c=c_{1}\;$ dla p-p i $c=c_{2}\;$ dla n-n

(1.33)

• gdzie: p-p to oznacza parzysto-parzyste, a n-n to nieparzysto-nieparzyste.

Model kroplowy opisuje średnie własności jader atomowych, ale nie opisuje jej struktury. Nasz model należy stosować dla jąder atomowych $A\geq 30\;$, a dla jąder $A\geq 40\;$ opisuje je z dokładnością do 2%.

Model gazu Fermiego

Protony i neutrony są to cząstki niezależne, które poruszają się niezależnie wewnątrz kuli o promieniu R=r₀A^1/2 (patrz: (1.28)), co stanowi, że pomiędzy tymi nukleonami nie ma wzajemnych oddziaływań. Nukleony są to fermiony zajmujące stan najniższy jak tylko możliwe ze względu na zakaz Pauliego bez dostarczania energii zewnątrz, co oznacza, że nukleony nie mogą się zderzać wzajemnie. Nukleony znajdują się w studni potencjału, a na każdym jego stopniu mogą znajdować się co najwyżej dwa nukleony. Energia najniższego poziomu jest to energia Fermiego, co rachunki pokazują, że średnia energia kinetyczna na tym poziomie jest E_k=30 MeV, czemu odpowiada średni pęd <p>=240 MeV/c, który zwany jest pędem Fermiego. Potwierdzenie pędu Fermiego pokazuje, że zderzenie jego z pociskiem z nukleonami w jądrze atomowym mówi, że pędy nukleonów są rozłożone izotropowo w nim, dlatego ten model jądra atomowego tak jest zwany.

Model powłokowy

Jądra, które nie można opisać za pomocą modelu kroplowego lub modelu gazu Fermiego wskazują, że jeśli kwanty powstałe w wyniku przejścia z jednego poziomu do drugiego są widmami dyskretnymi (liniowymi), co wskazuje na to, że stany w jakim znajdują się protony i neutrony nie są stanami ciągłymi, tylko dyskretnymi. Badanie pewnych jąder wskazują, że w przyrodzie występują nuklidy o pewnych liczbach protonów lub neutronów. Dalsza analiza B/A wskazuje na pewne maksima przy pewnych liczbach protonów i neutronów zwanych liczbami magicznymi.

Energia wiązania jąder atomowych a jego stabilność

(Rys. 1.3) Ścieżka stabilności dla wszystkich izotopów znanych lub występujących w przyrodzie. Linia pozioma to oś Z, a pionowa oś N

Dla jąder izobarycznych najsilniej związane są jądra o najmniejszej masie, izobary te są stabilne ze względu na rozpad β ale mogą być niestabilne ze względu rozpad α, sf. Nuklidy występująca nad linią Z=N są niestabilne ze względu na rozpad β^-, a nuklidy znajdujące pod ścieżką stabilności są to nuklidy ze względu na rozpad β⁺. Najcięższe znajdujące się nuklidy są to nuklidy, które podamy w tabelce poniżej w raz czasami ich rozpadu, które są jądrami niestabilnymi ze względu na rozpad α i samoistnie rozszczepienie:

Nuklid	Czas połowicznego rozpadu	Skład procentowy występowania danego nuklidu w skład danego pierwiastka w przyrodzie.
${}_{90}^{232}{\hbox{Th}}$	$1,4\cdot 10^{10}{\mbox{ lat}}\;$	100%
${}_{92}^{234}{\hbox{U}}\;$	$2,5\cdot 10^{5}{\mbox{ lat}}\;$	0,005%
${}_{92}^{235}{\hbox{U}}\;$	$7,0\cdot 10^{8}{\mbox{ lat}}\;$	0,72%
${}_{92}^{238}{\hbox{U}}\;$	$4,5\cdot 10^{9}{\mbox{ lat}}\;$	99,27%

Jadra ${}_{92}^{235}{\hbox{U}}\;$ i ${}_{92}^{238}{\hbox{U}}\;$ są używane w energetyce jądrowej. Najcięższym nuklidem stabilnym znanym przez człowieka jest ${}_{82}^{208}{\hbox{Pb}}_{126}\;$, których jest w 52,4% wchodzących w skład pierwiastka ołowiu, a także ${}_{83}^{209}{\hbox{Bi}}_{126}\;$, w których jest 100% wchodzących w skład pierwiastka bizmutu. Łącznie odkryto ponad 3000 nuklidów, co większości jąder są jądrami niestabilnymi.

Nuklidy stabilne i niestabilne

Przestawimy teraz tabelkę przedstawiający liczbę jąder stabilnych przy pewnej liczbie protonów i neutronów w jądrze w zależności od ich parzystości lub nieparzystości, dla jąder których czas połowicznego rozpadu jest większy od czasu życia ziemi, dla której czas trwania ziemi jest większy od $4,5\cdot 10^{9}{\mbox{lat}}\;$:

	Jadra o nieparzystej liczbie neutronów	Jądra o parzystej liczbie neutronów	Razem
Jądra o nieparzystej liczbie protonów	4	50	54
Jądra o parzystej liczbie protonów	55	165	220
Razem	59	215	274

Najcięższe nuklidy występujące na Ziemi w warunkach naturalnych są niestabilne ze względu na rozpad α i sf. Jądra stabilne lekkie to są dla $N\simeq Z\;$, a ciężkie $N\simeq 1,5Z\;$. Znanymi nuklidami nieparzysto-nieparzystych są to nuklidy:${}_{1}^{2}D_{1}\;$,  ${}_{3}^{6}Li_{3}\;$,  ${}_{8}^{10}B$,  ${}_{7}^{14}N\;$. Teraz podamy tabelkę superciężkich nuklidów wytwarzanych w laboratorium wraz z niektórymi reakcjami syntezy tychże jąder.

Rok odkrycia	Nuklid	Czas połowicznego życia	Reakcja uzyskania danego nuklidu
1996 rok	${}^{269}110\;$	170μs
	${}^{271}110\;$	1,1 ms
	${}^{272}111\;$	1,5μs
1998/99 rok	${}^{277}{112}\;$	0,24ms
	${}^{283}112\;$	81s
	${}^{289}114\;$	30s	${}_{20}^{48}Ca+{}_{94}^{244}Pu\rightarrow {}^{289}114+3n\;$
1999rok	${}^{289}116\;$	1,2s
	${}^{293}118\;$	250μs	${}_{36}^{86}Kr+{}_{82}^{208}Pb\rightarrow {}^{293}118+n\;$

Reguła Mattaucha (z doświadczenia)

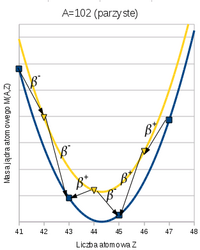
Jeśli energie wiązania jądra atomowego (1.7) (w której występuje wielkość niedoboru masy (1.6)) przedstawimy jako funkcję zmiennej Z dla jąder izobarycznych, ale dla A nieparzystego energię wiązania jądra atomowego układają się w parabolę, w której wystepuje jeden izotop (izobar) stabilny. Gdy natomiast A jest parzyste, to energia wiązania układa się w dwie parabole odpowiadające izobarom p-p, n-n, w tym przypadku może być więcej niż jeden izobar stabilny, a tych izobarów niestabilnych może być aż trzy. Pozostałe izobary (niestabilne) są niestabilne ze względu na rozpady β^-, β⁺ i EC.

(Rys. 1.4) Masy jąder w MeV o ustalonych liczbie masowej A=102

(Rys. 1.5) Masy jąder w MeV o ustalonych liczbie masowej A=135

Dla rysunków podano masy jąder atomowych w MeV w zależności od liczby atomowej jako przykład dla jądra o A parzystego, w której występują dwie gałęzie paraboli, a także podano następny przykład dla jądra A nieparzystego, w której występuje jedna gałąź paraboli. Liczbę Z₀ dla której funkcja B(Z,A=const) osiąga maksimum względem Z, podobnie przy M(Z,A=const) osiąga minimum względem Z, możemy obliczyć z:

$\left({{\partial B(Z,A)} \over {\partial Z}}\right)_{A=\operatorname {const} }=0\;$

(1.34)

i zgodnie ze wzorem Weizsäcker'a, gdy funkcja B(Z,A) jest przestawiona wzorem (1.23), to maksimum funkcji energii wiązania jądra atomowego jest określona dla liczby atomowej:

$Z_{0}={{A} \over {1,98+0,015A^{{2} \over {3}}}}\;$

(1.35)

Widzimy, że maksimum funkcji B(Z,A=const) jest zależne tylko od liczby masowej A. Możemy napisać dla ścieżki stabilności ze względu na rozpad β wzór empiryczny Greena:

$(N-Z)_{\beta \operatorname {stabilne} }={{0,4A^{2}} \over {A+200}}$

(1.36)

Rozpraszania wysokoenergetycznych cząstek e, p, n i innych cząstek na jądrze atomowym

Cząstki e, p, n te są traktowane jako sondy wynikające do wnętrza jąder. Ich kąt rozproszenia θ będzie uwarunkowany rozkładem gęstości centrów rozpraszających w jądrze, który uwarunkowany jest rozkładem masy i ładunków w naszym badanym obiekcie. Do badania rozkładu ładunku elektrycznego najlepiej do tego służą elektrony, ponieważ one kulombowsko oddziaływają z protonami, a więc daje ta metoda czystą informację o rozkładzie ładunku elektrycznego w jądrze ρ_e(r).

Relacje rozpraszania neutronów na jądrach atomowych dostarczają o rozkładzie masy w jądrze ρ_m(r). Realizacja tego projektu jest bardzo kłopotliwa ze względu na trudności z uzyskania wysokoenergetycznych neutronów.

Relacje rozpraszanie protonów p są najtrudniejsze do interpretacji wyników doświadczalnych, gdyż oddziaływają one z jądrem atomowym ze względu na to, że ten obiekt posiada ładunek elektryczny, czyli oddziałuje kulombowsko odpychająco z jądrem atomowym i też za pomocą sił jądrowych i takie rozpraszanie dostarcza zarówno informacje o rozkładzie masy i ładunku wewnątrz jądra.

(Rys. 1.6) Rozpraszanie cząstki na przestrzennym rozkładzie ładunku (masy)

Aby cząstka mogła wniknąć do jądra atomowego, to powinna mieć długość fali de Broglie'a odpowiednio małą do rozmiarów badanego jądra. Przelicznik długości fali w zależności od jej energii padającej na jądro atomowe wyraża się wzorem:

$\lambda _{e}={{200} \over {E_{e}(MeV)}}fm\;$

(1.37)

• dla $E_{e}=500MeV\;$ mamy $\lambda _{e}=0,4fm\;$.

Jeśli ładunek byłby skupiony w jednym punkcie, to różniczkowy przekrój czynny dla cząstek o energii E na jądrach o liczbie atomowej Z jest napisany wzorem Motta:

$\left({{d\sigma (E_{e})} \over {d\Omega }}\right)_{M}=\left({{Ze^{2}} \over {2E_{e}}}\right)^{2}{{\cos ^{2}{{\theta } \over {2}}} \over {\sin ^{4}{{\theta } \over {2}}}}\left(1+{{2E_{e}} \over {m_{e}c^{2}}}\sin ^{2}{{\theta } \over {2}}\right)\;$

(1.38)

Jeśli uwzględnimy rozkład przestrzenny ładunku elektrycznego w rzeczywistym jądrze atomowym, to według przybliżenia Borna pierwszego rzędu (mały ładunek jądra atomowego) piszemy według:

${{d\sigma (E_{e})} \over {d\Omega }}=\left({{d\sigma (E_{c})} \over {d\Omega }}\right)_{M}|F(q)|^{2}\;$

(1.39)

Tzn. wzór Motta ulega modyfikacji przy udziale czynnika kształtującego, który zależy od gęstości ładunku w tymże obiekcie wiedząc, że q jest pędem przekazywanym jądru (w jednostkach $\hbar \;$) w wyniku zderzeń:

$F(q)={{4\pi } \over {Zeq}}\int _{0}^{\infty }\rho _{e}(r)\sin(qr)rdr\;$

(1.40)