Wstęp do fizyki jądra atomowego/Rozpady (przejścia, przemiany) jądrowe
Licencja
|
|---|
|
Autor: Mirosław Makowiecki
Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność. |
Podręcznik: Wstęp do fizyki jądra atomowego.
Ogólny schemat rozpadów[edytuj]
Procesy zachodzące spontanicznie z powodów określonych oddziaływań pomiędzy nukleonami, w wyniku której jądro znajduje się w stanie quasistacjonarnym, to jądro przechodzi do stanu niższego energetycznie, ewentualnie emitując cząstkę unoszącą energię rozpadu. W końcowym etapie w wyniku czego jądro przechodzi w stan stacjonarny, które jest jądrem stabilnym w stanie podstawowym. Rozpad

jest dozwolony, jeśli spełnione są warunki opisane poniżej:
Warunek energetyczny[edytuj]
Wynika on z praw zachowania energii, dla jąder X i Y i cząstki ai będących w stanach podstawowych, to z tej zasady dla problemu mas wynika wniosek, że suma mas substratów w przemianie jądrowej powinna być większa niż suma mas produktów:

lub gdy jądra są w stanie wzbudzonym, wtedy dla problemu mas zachodzi suma masy substratów (jądra X) i jej energii wzbudzenia powinna być większa niż suma mas produktów Y, ai i energii wzbudzenia jądra Y:

Powyżej wyraziliśmy masę i energię w tych samych jednostkach, tzn. przy definicji prędkości światła równej jeden c=1. Energią rozpadu nazywamy wyrażenie, które jest różnicą masy jądra X przed rozpadem, i sumą masy jądra Y po rozpadzie i masy cząstek wyemitowanych:
![{\displaystyle M(X)-\left[M(Y)+\sum _{i}m_{a_{i}}\right]=Q\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad8ef00c0c475733ec57e7b91618a85db08d94e7)
- gdzie: M(X), M((Y) są masami odpowiednich nuklidów, które unoszą energię w postaci energii kinetycznej, tzn. energia rozpadu jest sumą energii kinetycznej jądra Y i cząstek ai:

Jeśli emitowana jest jedna cząstka, to ma określoną energię (widmo energii jest liniowe), a energia odrzutu jest w przybliżeniu zerowa, bo ma<<M(Y).
Reguły wyboru[edytuj]
Prawa zachowania momentów pędów przestawiamy jako sumę momentów pędu substratów, która jest równa sumie momentów pędu produktów w rozpadzie jądrowej, tzn. moment pędu jądra X przed rozpadem jest równy sumie momentów pędów cząstek ai i jądra Y:

Zasadę zachowania parzystości w naszym rozpadzie, oraz wartość momentu pędu cząstek ai możemy napisać, gdy suma momentów pędu naszych cząstek jest większa niż wartość bezwzględna różnicy momentów pędu jąder X i Y oraz mniejsza niż wartość sumy momentów pędów, a parzystość cząstki X przed rozpadem jest równa iloczynowi parzystości jądra Y i cząstek ai dla wszystkich „i”:


Prawo zachowania ładunku elektrycznego, ładunku barionowego i innych liczb kwantowych[edytuj]
Prawo zachowania ładunku elektrycznego i barionowego, taki że ładunek elektryczny lub barionowy przed i po rozpadzie zachowuje swoją wartość licząc względem wszystkich cząstek przed i po reakcji, przedstawiamy:


Klasyfikacja rozpadów[edytuj]
Ze względu na emitowane cząstki[edytuj]
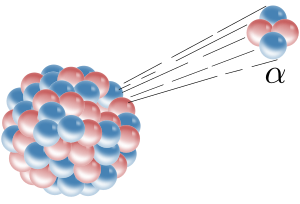
Rozpad α[edytuj]
W tym rozpadzie cząstka 



Rozpady β[edytuj]
w tym rozpad β- w którym powstaje jądro o liczbie atomowej zwiększonej o jeden, a także elektron (cząstka β-) wraz antyneutrinem elektronowym:

w tym rozpad β+, w którym powstaje jądro o liczbie atomowej zmniejszonej o jeden, a także pozyton (cząstka β+, elektron o ładunku dodatnim) wraz z neutrinem elektronowym:

Rozpady nukleonowe p i n[edytuj]
- rozszczepienie spontaniczne sf w wyniku czego powstają dwa jądra atomowe wraz z pewną liczbą neutronów:

Przejścia γ[edytuj]
Rozpad, w którym jądro wzbudzone przechodzi do stanu podstawowego ze stanu wzbudzonego z emisją kwantu γ:

Konwersja wewnętrzna (KW)[edytuj]
Ze względu na oddziaływania prowadzące do rozpadu[edytuj]
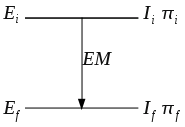
- przejścia elektromagnetyczne (EM): γ, KW, KP (deekscytacja jądra, jest to przejście jądra, ze stanu wzbudzonego do stanu podstawowego, przy czym jest zachowana liczba masowa A i atomowa Z jądra atomowego)
- przejścia (rozpady) słabe (beta): β-, β+, EC
- przejścia (rozpady) z udziałem oddziaływania silnego (jądrowego): α, p, n, sf.
Prawdopodobieństwo rozpadu (przejścia) ze stanu początkowego |i>[edytuj]
Wedle przypadku ogólnego stan quasistacjonarny może przejść w wyniku różnych procesów (rozpady jąder na końcowe jądra korzystne energetycznie). Stała rozpadu całego procesu jest sumą poszczególnych rozpadów, dla oddziaływań elektromagnetycznych λem, słabego λsl, i silnego λs:

Poszczególne stałe rozpadu definiujemy wedle schematów poniżej przy pomocy stałej zaniku przejścia elektromagnetycznego, która jest sumą rozpadów γ, konwersji wewnętrznej KW i deekscytacji jądra, ta stała jest w postaci:

Stała zaniku przejścia zachodzących w wyniku oddziaływań słabych jest sumą rozpadów β-, β+ i EC:

Stała zaniku przejścia zachodzących w wyniku oddziaływań silnych jest sumą stałych zaniku rozpadu α, rozczepienia spontanicznego sf i przejść nukleonowych p i n.

Średni czas życia danego rozpadu lub wszystkich rozpadów (3.16) definiujemy jako odwrotność stałej zaniku danego rozpadu lub wszystkich rozpadów:

Czas życia, danego rozpadu ze względu na dany typ rozpadu, w którym cząstka ze stanu |i> przechodzi w stan |f>, jest określany:

Stała rozpadu, nie zależy od warunków zewnętrznych, historii rozpadu, jest to wielkość stała charakteryzująca dany proces. W kwantowej teorii zaburzeń stała rozpadu przejścia ze stanu „i” do „f”, znając gęstość stanów ρf(E), w której zawarta jest zależność stałej rozpadu od energii emitowanych cząstek E, a także hamiltonian Hif, który jest odpowiedzialny za przejście od stanu „i” do stanu „f”, które jest traktowane jest jako zaburzenie, jest zapisana:

- gdzie:
– gęstość stanów końcowych w jednym przedziale dozwolonym energetycznym.
– ta część hamiltonianu oddziaływania, który jest odpowiedzialny za dane przejście, traktujemy go jako zaburzenie.
To samo prawo stosujemy do cząstek elementarnych, stanów wzbudzonych atomów, itp., tzn. do rozpadów kwazistacjonarnych, które są układami kwantowymi.
Prawo rozpadu[edytuj]
Prawdopodobieństwo rozpadu, czyli iloraz liczby cząstek rozpadających się dN i liczby cząstek nierozpadniętych N, jest wprost proporcjonalne do czasu, w którym ten rozpad jest dokonywany, tzn.:

Wyznaczmy teraz czas, w którym liczba cząstek zmniejsza się „e” razy względem jej liczby w czasie równym zero (N(0)), czyli:

Wyznaczmy średni czas rozpadu z definicji wartości średniej względem czasu:

Udowodniliśmy, że średni czas zaniku jest odwrotnością stałej zaniku λ, czyli jest równy czasowi τ, po którym liczba cząstek maleje e razy. Wyznaczmy teraz czas połowicznego zaniku (półokres rozpadu), w którym liczba cząstek zmniejsza się o połowę względem czasu podstawowego N(0), patrząc na wynik (3.24) i (3.25), otrzymujemy, że czas połowicznego zaniku jest równy czasowi, której liczba cząstek zmniejsza się e razy względem N(0) pomnożonej przez logarytm naturalny liczby dwa:

Rozkład sukcesywny nazywamy proces:

Mechanizm rozpadu (przemiany) α[edytuj]
Wyniku rozpadu jądra X o liczbie masowej A i atomowej Z z jądra wylatuje w wyniku zjawiska tunelowania cząstka 

Energia pomiędzy stanami podstawowymi jąder 

![{\displaystyle Q_{\alpha }=M(A,Z)-\left[M(A-4,Z-2)+M(\alpha )\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52056ebc597386f2ab4c235ce293830f43d5a4ae)
Warunkiem koniecznym zaistnienia rozpadu (3.28) jest warunek konieczny Qα>0. Warunek (3.29) jest spełniony dla jąder, dla której stosunek B/A=f(A) leży w opadającej części wykresu, tzn. dla jąder ciężkich o A≥150, które znajdują się w stanach podstawowych. Energia rozpadu Qα jest unoszona w postaci energii kinetycznej jądra Y i energii kinetycznej cząstki α. Widmo energetyczne cząstki α jest liniowe i jego energia mieści się w zakresie 4MeV≤Eα≤9MeV. Wartość momentu pędu cząstki α jest większa od wartości bezwzględnej różnicy jądra X i Y i jest mniejsza niż suma wartości momentów pędu cząstki X i Y:

Parzystość cząstki α, jest iloczynem parzystości jądra X i jądra Y, jest wyrażona:

Rozpad α jest uwarunkowany oddziaływaniem silnym, i cząstka α by pokonać barierę potencjału, dla którego zachodzi Eα<Ebariery potencjału ulega zjawisku tunelowania, co jest zgodne z mechaniką kwantową, w wyniku czego jądra helu wydostaje się z jądra X z pewną energią Eα. Potencjał V(r) jądra atomowego wyrażamy przez sumę energii związanych z energią kulombowską i energią związaną z momentem pędu wynikających z równania własnego operatora energii, jest ona równa pisząc je ogólnie dla 



Współczynnik przenikalności bariery potencjału jądra X[edytuj]
Współczynnik przenikalności bariery wyrażamy przy pomocy potencjału oddziaływania kulombowskiego VC i potencjału związanego z momentem pędu Vl i piszemy go:

Prawdopodobieństwo rozpadu α[edytuj]
Stała rozpadu jest iloczynem prawdopodobieństwa utworzenia cząstki α w stanie quasistacjonarnym Pα, który aby obliczyć należy znać strukturę jądra atomowego, ono nie zmienia się silnie od jądra do jądra, przez częstość ν:

- gdzie „t” czas, w którym cząstka α przebiega jądro.
i przez współczynnik przenikalności bariery D (3.33), stała rozpadu α, czyli λα jest napisana:

Zwykle przyjmuje się k=Pαν≈1020, to stała rozpadu (3.35) ma wzór λα=k⋅D.
Prawo Geigera-Nutalla[edytuj]
Jest to zależność pomiędzy czasem T1/2 połowicznego rozpadu jądra X, co wyniku tego ono emituje cząstkę α, a energią cząstek α Eα, wyrażona przy pomocy stałych C(Z) i D(Z) zależnej od liczby atomowej Z:

Zależność stałej C i D od liczby atomowej przedstawia tabela:
| Z | C | D | Z | C | D |
|---|---|---|---|---|---|
| 84 | -50,15 | 128,8 | 92 | -52,55 | 143,1 |
| 86 | -50,94 | 132,7 | 94 | -53,35 | 147,4 |
| 88 | -51,51 | 136,2 | 96 | -53,97 | 151,3 |
| 90 | -51,94 | 139,4 | 98 | -54,40 | 154,7 |
Prawidłowość (3.36) ustalili doświadczalnie w latach 1911–1912 uczeni H. Geiger i J. Nutall, a następnie w 1928 uzyskali ją opierając się na kwantowym opisie procesu rozpadu α. Ten wzór opisuje proces rozpadu α. Wzór najdokładniej opisuje rozpady jąder dla jąder parzysto-parzystych. Stałe C i D zależą nieznacznie od liczby atomowej, co ilustruje powyższa tabelka.
Rozpady nukleonowe[edytuj]
- Rozpad neutronowy, w którym jądro o liczbie masowej A i atomowej Z wysyła jeden neutron, w ten sposób zmniejsza on liczbę masową o jeden przy takiej samej liczbie atomowej:

- Rozpad protonowy, w którym jądro o liczbie masowej A i atomowej Z wysyła jeden proton, w ten sposób zmniejsza on liczbę masową A i atomową Z o jeden:

Warunek energetyczny (energia rozpadu)(N od n lub p)[edytuj]
- Jeśli oba jądra X i Y w (3.37) i (3.38) są w stanie podstawowym, wtedy energia rozpadu jądra unoszona przez neutrony jest równa:
![{\displaystyle Q_{N}=M_{j}(X)-[M_{j}(Y)+m_{N}]\geq 0\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c1cd0c46a621c7aa2720741b501c5fb60365e5b)
- Gdy jądro X rozpada się ze stanu wzbudzonego na jądro Y, to energia rozpadu, która jest zawsze większa niż zero, przedstawia się:
![{\displaystyle Q_{N}=M_{j}(X)+E_{wzb}-[M_{j}(Y)+m_{N}]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50db36c192048151ccc87a7d56dbde7727fbea1d)
- Gdy jądro X ze stanu wzbudzonego rozpada się na jądro w stanie wzbudzonym Y, dla której energia rozpadu jest zawsze większa niż zero, to ciepło rozpadu jest:
![{\displaystyle Q_{N}=M_{j}(X)+E_{wzb}(X)-[M_{j}(Y)+m_{N}+E_{wzb}(Y)]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6403077be166fc89b047744c64cf1ff1e3a601c5)
Przy rozpadzie ze stanów wysokoenergetycznych składa się on z bardzo wielu linii (wierzchołków), zauważmy jednak, że zachodzi:
- rozpadu nukleonowe są wynikiem oddziaływań silnych.
- jeśli jest spełniony warunek energetyczny (3.41), to jądro jest wzbudzone ze względu na jego spin i parzystość, i rozpad jego następuje z czasem połowicznego zaniku równej τ≈10-22s.
- rozpad protonowy może być zahamowany przez barierę kulombowską.
- jeśli energią protonu jest mniejsza niż wysokość bariery, to protony z takiego jądra wychodzą na zewnątrz niego poprzez proces tunelowania, tak jak w rozpadzie α.
- rozpady protonowe konkurują z rozpadami β+, EC,α, a rozpady neutronowe zachodzą z konkurencją β-. Pierwszy i drugi rozkład konkuruje z rozpadem elektromagnetycznym EM dla jąder X wzbudzonych.
Rozpady nukleonowe obserwuje się w jądrach neutrononadmiarowych (rozpad n) i w jądrach neutronodeficydowych (rozpad p). Rozpady nukleonowe obserwuje się jako rozczepienia w ciężkich jądrach wysoko-wzbudzonych neutrononadmiarowych oraz w wyniku rozpadu jąder dalekich od ścieżki jąder stabilnych. Rozpady nukleonowe konkurują z rozpadami elektromagnetycznymi, γ, i KP (deeskcytacją jądra atomowego).
Przemiana (rozpad) β[edytuj]
Neutron w jądrze rozpada się na proton, elektron i antyneutrino elektronowe, a proton w jądrze rozpada się na neutron, pozyton i neutrino elektronowe, te dwie przemiany piszemy:


Jeśli w jądrze atomowym zachodzi przemiana (3.42), to liczba masowa jądra się nie zmienia, a liczba atomowa Z zwiększa się o jeden, tą przemianę piszemy:

Jeśli w jądrze atomowym zachodzi przemiana (3.43), to liczba masowa jądra się nie zmienia, ale za to liczba atomowa zmniejsza się o jeden, tę przemianę piszemy:

- Warunki energetyczne rozpadu β-
Patrząc na rozpad (3.44) warunek na energię rozpadu, która jest większa lub równa zero, i jest wyrażona jako różnicę masy jądra 

![{\displaystyle Q_{\beta ^{-}}=M(A,Z)-[M(A,Z+1)+m_{e}+m_{{\tilde {\nu }}_{e}}]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58e49b57048f6023fdb4e4fdd5cc60c7c13a7fa5)
Wykorzystując wzór (1.16) na mass excess dostajemy wzór na ciepło rozpadu β-:

- Warunki energetyczne rozpadu β+
Patrząc na rozpad (3.45) warunek na energię rozpadu, która jest większa lub równa zero, jest wyrażona jako różnica masy jądra 

![{\displaystyle Q_{\beta ^{+}}=M(A,Z)-[M(A,Z-1)+m_{e}+m_{\nu _{e}}]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f622c9b6b2795be0c796bd36a0c23a6e4f6bd29)
Wykorzystując wzór (1.16) na mass excess dostajemy wzór na ciepło rozpadu β+:

- Przemiana EC
Te przemiany powstają po wychwycie elektronu lub pozytonu przez jądro i odpowiednio liczba masowa A nie zmienia się, a liczba atomowa Z maleje o jeden po wychwycie elektronu:

Energia rozpadu jest różnicą sumy masy jądra 

![{\displaystyle Q_{EC}=M(A,Z)+m_{e}-[M(A,Z-1)+m_{\nu _{e}}]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e077cfd31a957ce71d165a3291460a64e8a2ff7)
Rozpad β- i EC z wychwytem elektronu to są procesy konkurencyjne. Najbardziej prawdopodobny jest wychwyt elektronu z powłoki elektronowej K. Stała zaniku tejże przemiany jest sumą stałej zaniku powstałej z wychwytem elektronu z powłoki elektronowej K, który dominuje i z dalszych powłok elektronowych, nazwijmy je LI i LII, itd.

- W Jądrach lekkich stała zaniku przemiany EC λEC z wychwytem elektronu jest mniejsza lub równa stałej rozpadu przemiany β+ (λEC≤λβ+), w jądrach ciężkich stała zaniku λEC jest większa niż stała zaniku przemiany β+, (λEC>λβ+). Iloraz stałej zaniku przemiany EC przez stałą zaniku β+ jest wyrażony, w zależności od energii przemiany QEC (3.57) i liczby atomowej Z:

- Anihilacja elektronu i pozytonu
W wyniku zderzenia elektronu i pozytonu obie te cząstki znikają i pojawiają się dwa kwanty γ pędzące w przeciwnych kierunkach, gdzie energia pojedynczego kwantu jest Eγ=511keV.

Rozpadowi β+ towarzyszy emisja promieniowania anihilacyjnego γ. Procesowi EC z wychwytem elektronu towarzyszy emisja antyneutrinów elektronowych 
Energia wydzielana w rozpadzie β jest to energia wyrażona wzorem (3.46) (rozpad β-) lub (3.48) (rozpad β+), energia ta może być pomniejszona, gdy powstałe jądro po przemianie przejdzie w stan wzbudzony, wtedy 

Rysunek (Rys. 3.8) przedstawia widmo w rozpadzie beta, gdy nie uwzględnimy bariery potencjału.
Widmo energetyczne rozpadających cząstek jest ciągłe (powstają dwie cząstki). W rozkładzie β+ rzeczywiście nie ma pozytonów o zerowej energii, ponieważ w tym rozpadzie powstający elektron musi przebyć barierę energetyczną, w wyniku czego cząstka β+ zostaje rozpędzona do pewnej prędkości, co jest wynikiem odpychania kulombowskiego, widmo energii (Rys. 3.8) jest przesunięte w lewo, a w przepadku rozpadu β- widmo jest przesunięte w prawo, a więc w tym ostatnim nie ma cząstek o energii zerowej, ponieważ cząstka zostaje zwolniona przez barierę potencjału. Pomiary energii maksymalnej cząstki beta, czyli 

- Prawdopodobieństwo przejść
Zgodnie z elektrodynamiką kwantową prawdopodobieństwo przejścia na jednostkę czasu pomiędzy stanami <i| a <f| z emisją cząstki o energii (E,E+dE), który tutaj używając E0=Ee+Eν=Qβ, czyli ρf(E0) oznacza gęstość stanów końcowych e i ν, napiszemy:

- gdzie
jest to hamiltonian opisujący mechanizm oddziaływań słabych.
Wygodnie jest liczyć prawdopodobieństwo przemiany β w przedziale (p,p+dp) i mając na uwadze (3.57), to z niego otrzymujemy:

wtedy wzór na gęstość stanów końcowych jest równa 

Wiedząc, że 


Mając wzór na przelicznik pędu cząstki na jej energię całkowitą 


Jeśli dodatkowo będziemy pamiętać, że masa neutrina może być różna od zera, tzn. mν≠0, wtedy energia prawdopodobieństwa stanów przejścia, przeliczając znów gęstość prawdopodobieństwa stanów końcowych ρf(E0) dla tego przypadku, przedstawia się:

We wzorze (3.62) zauważmy, że zachodzi 
- Wpływ masy spoczynkowej lub jej brak dla (anty)neutrina na widmo elektronów w rozpadzie β
Należy porównać wzory na λ(E)dE z uwzględnieniem masy spoczynkowej neutrina i przy zerowej jego masie. W widmie elektronów istnieją różnice występujące na jego samym końcu, przy masie spoczynkowej neutrina różnej od zera, koniec widma jest prostopadły do osi Ee, a gdy masa neutrina jest równa zero, to koniec widma dąży stycznie do tej osi. Na podstawie widma można wyznaczyć masę spoczynkową neutrina mν. Wynik rozpadu β- na jądrze 3He, którego energia rozpadu jest Qβ=18,6keV i o czasie połowicznego rozpadu T1/2=12,3 lat wykazały, że masa spoczynkowa neutrina jest mniejsza niż 35eV (mν≤35eV).
- Wpływ pola elektrycznego jądra na stałą zaniku rozpadu β λβ i na widmo β
Pole elektryczne wpływa na wynik stałej zaniku w rozpadzie β, dlatego wprowadza się czynnik korekcyjny Fermiego, który jest ilorazem kwadratów modułów funkcji falowej fali płaskiej pod wpływem pola elektrycznego i cząstki swobodnej:

W przybliżeniu nierelatywistycznym czynnik korekcyjny Fermiego ma postać:

- gdzie we wzorze na X (3.64) wybieramy znak plus dla rozpadu β-, a dla rozpadu β+ znak minus. Jeżeli mν=0, to prawdopodobieństwo (3.61) przy uwzględnieniu czynnika korekcyjnego Fermiego:

Często Ee wyraża się jednostkach mec2, czyli przy podstawieniu 

Ale F(E,Z) można obliczyć jeszcze dokładniej uwzględniając efekty relatywistyczne, a także uwzględniając pole elektryczne powłok elektronowych. F(E,Z) posiada wartości zebrane w tablicach fizycznych.
- Całkowite prawdopodobieństwo przejścia
Wzory λβ(E) opisywały prawdopodobieństwo przejścia β między stanami 


które jest prawdopodobieństwem całkowitego przejścia i→f. Dla przejść dozwolonych zakładając przy tym, że 

Z drugiej jednak strony według (3.25) stała rozpadu jest odwrotnością średniego czasu rozpadu i odwrotnością czasu połowicznego rozpadu pomnożonej przez logarytm naturalny z dwójki:

Wzory (3.69) (na stałą zaniku w zależności od czasu połowicznego rozpadu) możemy połączyć ze wzorem (3.68) (na definicję stałej zaniku z teorii rozpadu β), w ten sposób otrzymując:

Wartości ft są bardzo duże, więc przyjęto się podawać jego logarytm log ft, praktycznie ono mieści się w przedziale 3≤log ft≤22, co odpowiada czasom połowicznego zaniku ∼10-3s≤T1/2≤∼1014lat
 , i parzystości: , i parzystości:  . . | |||
 to stopień wzbronienia, wtedy zmiana parzystości: to stopień wzbronienia, wtedy zmiana parzystości:  , i momentu pędu: , i momentu pędu:  (nieunikalne) lub (nieunikalne) lub  (unikalne). (unikalne). | |||
Elementy macierzowe hamiltonianu w rozpadzie β względem stanu krańcowych (elementy teorii rozpadu β)[edytuj]
Teorię rozpadu β opracował E. Fermi w roku 1934 r., według której ten rozpad jest wynikiem oddziaływań słabych nukleonu z polem elektronowo-neutrinowym w jądrze atomowym.
W tym modelu wprowadzono, że oddziaływanie słabe jest superpozycją pięciu oddziaływań cząstkowych, w tym: oddziaływania skalarnego (S), wektorowego (V), tensorowego (T), pseudowektorowego (A) i pola pseudoskalarnego (P). Każdej postaci oddziaływania odpowiada określona postać hamiltonianu 





Funkcje falowe 


- W uproszonym modelu przyjmuje się, że te funkcje są jednoskładnikowe i dla e i ν funkcje falowe opisujące je są funkcjami typu fali płaskiej:

- Parzystość jest zachowywana, gdy
, jest równe zero.
- operator zaburzenia dla wszystkich oddziaływań jest wielkością stałą
, gdzie g charakteryzuje natężenie (ładunek) oddziaływania słabego.
Na podstawie powyższych uproszczeń mamy kwadrat elementu macierzowego operatora (3.71):

- Element macierzowy Mif nazywamy jądrowym elementem macierzowym. Wzór (3.73) określa prawdopodobieństwo kreacji pary (e,ν) w jądrze. Funkcja (3.72) słabo zależy od r dla r≤Rj, więc możemy przyjąć:

Wartość Mif zależy od stopnia pokrycia się fal stanów końcowych 


Taką sytuację mamy w jądrach lekkich (Z=N) i w jądrach zwierciadłowych. W jądrach tychże prawdopodobieństwo przejścia β zachodzi z dużym prawdopodobieństwem (logft∼ od 3 do 3,5, co je nazywamy przejściami ponaddozwolonymi) i |Hif|2 nie zależy od energii cząstek β Eβ.
- Ogólnie |Hif|2, a więc i λi→f, a zarazem log ft zależą od
(plus człony mieszane), a więc od rodzaju oddziaływania (k) i od struktury stanów jądrowych
,
.
Z porównania wyników doświadczalnych (wykresów Fermiego-Kurie,lopgft, itp.) z obliczeniami teoretycznymi (wg. Fermiego) wynika, że:
- Oddziaływania S i V jest oddziaływaniem kreującym parę leptonów (elektronu i neutrino) w stanie singletowym (o przeciwnych spinach), stąd wynika, że zachowana jest orientacja spinu nukleonu biorącego udział w przemianie β, stąd regułami wyboru są:


- Oddziaływania T (tensorowe) i A (pseudowektorowe), czyli inaczej zwane oddziaływaniem Gamowa-Tellera, kreują parę e i ν w stanie tripletowym (spiny e i ν są ze sobą zgodne), wtedy zmienia się orientacja spinu nukleonu na przeciwny. Regułami wyboru w tym przypadku są przedstawione poniżej za wyjątkiem przejścia 0⇒0, który jest niedozwolony:


- Za rozpady β są odpowiedzialne oddziaływania typu V i A, tzn. kwadrat elementy macierzowego jest równy:

Stosunek stałej gA przez stałą gv jest równy: 

Stałą gk można wyznaczyć znając wartość log ft ze wzoru (3.70), a stąd wyznaczamy 
Niezachowywanie parzystości w rozpadzie β[edytuj]
Funkcję nazywamy parzystą, gdy po zamianie w niej wektora położenia na minus, otrzymamy ten sam wektor, a wartość funkcji nie zmienia się. Funkcję nazywamy nieparzystą, gdy wartość funkcji zmienia się na przeciwną, całą teorię funkcji parzystych i nieparzystych podano w książce Transformacja inwersji przestrzeni a prawo zachowania parzystości. Dotychczas uważano, że zasada zachowania parzystości jest spełniona zawsze i jest na równi z zasadą zachowania energii, ale T.D Lee i L.N. Yang (1956 r.) wykazali, że można zbudować teorię rozpadu β, w której nie jest spełniona zasada zachowania parzystości. Sugerowali, że ewentualne niezachowanie parzystości można wykryć badając jądra spolaryzowane w rozpadzie β, która jest domeną oddziaływań słabych.
- Doświadczenie C.B. Wu ze współpracownikami
W tym doświadczeniu badano emisję cząstek β ze spolaryzowanych jąder 60Co, w celu wyznaczenie wartości średniej pseudoskalara 




W tym doświadczeniu temperaturę T≈10-3 uzyskano metodą adiabatycznego rozmagnesowania paramagnetyka, uprzednio ochłodzonego do temperatury 1K, tzn. do temperatury ciekłego He pod zmniejszonym ciśnieniem. Pole B=10T uzyskano dzięki wykorzystaniu wewnętrznych pól magnetycznych paramagnetyków (azotanu cezowo-magnezowego), które polaryzowano małym polem zewnętrznym. Moment magnetyczny 60Co jest μ≈3,8μN. W doświadczeniu uzyskano więcej emitowanych elektronów β- w kierunku przeciwnym do orientacji spinu 60Co, stąd wynika, że parzystość nie jest zachowana. Funkcja kątowa rozkładu β- jest:

Wzór (3.82) wyjaśnia anizotropowy rozkład kątowy cząstek β-.
Skrętność leptonów[edytuj]
Następna grupa pomiarów dotyczyła pomiaru polaryzacji elektronów i neutrin w celu określenia polaryzacji pędu 


Elektrony z rozpadu β są spolaryzowane podłużnie. Skrętność νe wyznaczono w doświadczeniu Goldhabera, ustalono, że skrętność elektronu jest He-=-1, dla pozytonu He+=+1, dla neutrina elektronowego Hνe=-1 i antyneutrina elektronowego 
Przejścia elektromagnetyczne (emisyjne)[edytuj]
Przejścia elektromagnetyczne dzielimy na:
- przejścia γ, emitowany jest kwant γ, jego stała zaniku jest λγ.
- przejścia konwersyjne (KW) emitowany jest elektron e-, jego stała zaniku jest λKW.
- przejścia konwersyjne z zachowaniem pary e+e- (KP), jego stała zaniku jest λKP.
Całkowita stała zaniku przejść elektromagnetycznych jest sumą stałych zaniku wcześniej wymienionych trzech przejść, tzn.:

Wprowadźmy nowe oznaczenia, tzn.
jako całkowity współczynnik konwersji wewnętrznego danego przejścia.
jako współczynnik konwersji z utworzeniem pary e+e-
Wzór (3.90) na podstawie wcześniejszych oznaczeń przyjmuje postać:
![{\displaystyle \lambda _{EM}(i\rightarrow f)=\lambda _{\gamma }(i\rightarrow f)\left[1+\alpha _{t}(i\rightarrow f)+\alpha _{KP}(i\rightarrow f)\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50f3cdc185f19444c20fb66239c4484e5ffb252b)
Promieniowanie towarzyszące poszczególnym przejściom unosi energię Ei-Ef, moment pędu 
Przejścia γ[edytuj]
Dzięki energii przejścia emitowany jest kwant γ o energii Eγ i częstości ν, czyli Eγ=hν=Ei-Ef-Eod, gdzie energia odrzutu 
- moment pędu
o wartości jego kwadratu momentu pędu
.
- parzystość πE=(-1)l w przypadku pola elektrycznego, lub πM=(-1)l+1 w przypadku pola magnetycznego.
- Rodzaj pola (σ≡E lub M) i rząd polowości (l) promieniowania określa się wspólnym mianem multipolowością (σl), co bardziej ogólniej można powiedzieć, że multipolowość jest parametrem każdego przejścia EM wynikający z reguł wyboru i własności pola EM jądra.
- Reguły wyboru przejścia elektromagnetycznego
Moment pędu promieniowania elektromagnetycznego jest większy od wartości bezwzględnej różnicy wartości momentów pędu poszczególnych jąder krańcowych (jądro przed i po rozpadzie), dalej ona jest natomiast mniejsza od sumy krańcowych momentów pędu jąder:

Parzystość unoszona przez kwant γ jest:

Ponieważ nie ma promieniowania monopolowego l=0 przejścia typu Ii=0→If=0 są wzbronione.
- Szereg multipolowy
Szereg multipolowy promieniowania γ jest zawsze szybkobieżny ze względu na l, bo stosunek stałej zaniku dla ściśle określonego promieniowania dla l i l+1 jest równy 105, a także stosunek stałej zaniku promieniowania elektrycznego i stałej zaniku w promieniowaniu magnetycznemu jest równy od 10 do 100, czyli liczbie masowej podniesionej do kwadratu i spierwiastkowanej o stopniu trzy, te dwa wzory przedstawiamy:


Promieniowanie Ml może być zmieszane z promieniowaniem z El+1 i procentowemu udziałowi wyższej polowości promieniowania elektrycznego lub magnetycznego określa współczynnik określony w procentach:

Na przykład promieniowanie M1 może być zmieszane z 10% promieniowania E2 lub inny przykład E1+0,01%M2, to stopień zmieszania określa się przez współczynnik zmieszania danego przejścia jako:

- Prawdopodobieństwo przejścia
Prawdopodobieństwo przejścia ze stanu końcowego o stałej zaniku λ(σl,i→f) określamy znając energię przejścia Eγ:
![{\displaystyle \lambda (\sigma l,i\rightarrow f)={{8\pi } \over {\hbar }}{{l+1} \over {l[2l+1]!!]^{2}}}\left({{E_{\gamma }} \over {\hbar c}}\right)^{2l+1}B(\sigma l,i\rightarrow f)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbf7654b826b1daa7482b1ab8ac5299a81ce391c)
- gdzie zredukowane prawdopodobieństwo przejścia
dla ściśle określonego danego rodzaju promieniowania elektromagnetycznego jest zapisane:

- gdzie
jest to zredukowany element macierzowy multipolowego operatora
przejścia o multipolowości σl.
Konwersja wewnętrzna (KW)[edytuj]
Przejście elektromagnetyczne, w którym energia przejścia Ei-Ef zostaje przekazana elektronowi z powłoki n o energii wwiązania Be<Ei-Ef, W wyniku czego elektron wylatuje z energią kinetyczną równą:

Konwersja wewnętrzna jest możliwa, gdy funkcje falowe powłoki elektronowej o numerze „n” i funkcje falowe jądra pokrywają się częściowo. Przykrycie to maleje ze wzrostem liczby powłoki „n”, a stąd powinno zachodzić:

Prawdopodobieństwo danej całkowitej konwersji wewnętrznej podczas przejścia i→f przy wybiciu odpowiednich elektronów z powłok elektronowych (K,L,M,...) jest równe:

KW towarzyszy emisja EKW oraz promieniowania X lub elektronów Augera. Widmo energii wybijanych elektronów jest dyskretne.
- Reguły wybory
Moment pędu promieniowania elektromagnetycznego jest większa od wartości bezwzględnej różnicy wartości momentów pędu poszczególnych jąder krańcowych (jądro przed i po rozpadzie) i jest natomiast mniejsza od sumy momentów pędu jąder krańcowych, dalej przedstawiamy tą zależność jako:

Cząstki unoszą parzystość równą iloczynowi parzystości poziomów krańcowych „i” i „f” równą:

Dozwolone są przejścia 



Współczynnik kowersji wewnętrznej jest równy:

Wartości poszczególnych konwersji wewnętrznych dla powłoki elektronowej n przedstawiamy ogólnym wzorem αn(σl)if=f(n,Z,Eγ,σl). Dla przypadków przejść mieszanych σl+σ'l+1 dla dowolnej powłoki elektronowej, z której elektron jest wybijany, stałą zaniku określamy:

Współczynnik konwersji wewnętrznej WKW na podstawie stałej zaniku (3.100) przedstawiamy:

Jeśli wykorzystamy definicję współczynnika zmieszania 

Widać, że współczynniki WKW, że względu na powłokę, której zostaje przekazana energia elektronowi tam się znajdującej spełnia następującą relację:

![{\displaystyle =[\alpha _{K}(\sigma l)+\delta _{\gamma }^{2}\alpha _{K}(\sigma ^{'}+1)]:[\alpha _{L_{I}}(\sigma l)+\delta _{\gamma }^{2}\alpha _{L_{I}}(\sigma ^{'}+1)]:[\alpha _{L_{II}}(\sigma l)+\delta _{\gamma }^{2}\alpha _{L_{II}}(\sigma ^{'}+1)]:...\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67fcfc36a533c5fb66d15f030fd990287f94a60a)
Ogólne zasady pomiarów parametrów przejść elektromagnetycznych jąder atomowych[edytuj]
Energia przejścia Eif, współczynnik WKW przejść elektromagnetycznych, promieniowanie elektromagnetyczne zmieszane σl+σ'l', parametr zmieszania przejść γ δ2, a także zredukowany element macierzowy przejścia B(σl), wtedy zając te parametry można poznać strukturę jąder atomowych.
Energie przejść γ[edytuj]
Badania przejść elektromagnetycznych polega na badaniu:
- pomiaru widm promieniowania γ, tzn.: Eif, Eγ(-Eodrzutu)
- pomiaru widm EKW (konwersji wewnętrznej, tzn.:E=EEKW(n)+Be(n).
Aparaturę widm γ dzielimy na spektrometry γ (licznikowe i krystaliczne), spektrometry EKW (licznikowe i magnetyczne).
Multipolowość (σl+σ'l',δ2)[edytuj]
Multipolowość dla przejść γ(σl+σ'l',δ2) określa się na w sposób:
- na podstawie reguł wyboru, gdy określone są spiny i parzystość jąder
, gdy są określone warunki zmieszania promieniowania elektromagnetycznego σl+σl+1.
- a także z pomiarów bezwzględnych wartości WKW (3.99) i porównanie jej z doświadczeniem, ten współczynnik jest funkcją multipolowości i parametru zmieszania (3.91), wartość bezwzględna tego współczynnika jest stosunkiem ilości jąder ulegająca przemianie, tzn. konwersji wewnętrznej przez liczbę kwantów γ wydzielanych na przejściu z danego poziomu w jądrze na niższy:

- z pomiarów stosunków liczby cząstek ulegające konwersji wewnętrznej, które są według definicji przechwycenia przez jądro elektronu z powłoki LI, LII,LIII, tzn. NEKW(LI)/NEKW(LII)/NEKW(LIII), które są silną funkcją σ i δ2 dla przejść elektromagnetycznych. Określmy parametr zmieszania, który określa się przy pomocy współczynników konwersji wewnętrznej dla przejść pomiędzy LI i LII, czyli dla M1+E2 w sposób:

Podobne wzory otrzymujemy dla przejść LII i LI. Stosunki N(n)/N(n') określa się na podstawie widm EKW. Stosunki λLI/λLII,λLI/λLIII,λLII/λLIII silnie zależą od multipolowości σl i energii E przejścia. Pomiary tychże stosunków EKW na podpowłokach LI, LII, LIII, itd. pozwala wyznaczyć współczynniki Qγ i δ2.
Zredukowane prawdopodobieństwo przejścia[edytuj]
Zredukowane prawdopodobieństwo przejścia możemy określić przy pomocy wzoru (3.92). B(σl) możemy wyznaczyć z pomiarów λγ(σl). Dla rozważań nad zjawiskiem KP i przejściami γ, to całkowita stała zaniku określamy jako sumą stałej zaniku przejścia γ i przejścia konwersji wewnętrznej, czyli przejścia KP.

Wiedząc, że stała zaniku dla przejścia elektromagnetycznego λ'EM jest odwrotnością średniego czasu życia rozpadu elektromagnetycznego, to stałą zaniku przejścia γ piszemy przez:

Skorzystajmy ze wzoru (3.92), który przepiszemy dla przejrzystości wykładu:
 gdzie:
gdzie: ![{\displaystyle f(E_{\gamma },l)={{8\pi } \over {\hbar }}{{l+1} \over {l[2l+1]!!]^{2}}}\left({{E_{\gamma }} \over {\hbar c}}\right)^{2l+1}\;,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c34cab7833a6974b6e8d8eec4da21da18cc68f3)
Zredukowane prawdopodobieństwo przejścia według wzoru (3.109) określamy poprzez:

Ale dla przypadku przejść zmieszanych σl+σ'l+1 stałą zaniku promieniowania elektromagnetycznego dla multipolowości zmieszanych σl+σ'l+1 określamy jako sumę stałej zaniku promieniowania γ o tej multipolowości i stałej zaniku konwersji wewnętrznej też o tych samych zmieszanych multipolowościach, tutaj będziemy korzystać ze wzoru (3.109) i definicji stałej konwersji wewnętrznej αKW:
![{\displaystyle \lambda _{EM}(\sigma l+\sigma ^{'}l+1)=\lambda _{\gamma }(\sigma l+\sigma ^{'}l+1)+\lambda _{KW}(\sigma l+\sigma ^{'}l+1)=\lambda _{\gamma }(\sigma l+\sigma ^{'}l+1)\left[1+\alpha _{KW}(\sigma l+\sigma ^{'}l+1)\right]=\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48db86408659319c0c231e83ce36ec96931e914d)
![{\displaystyle =\left(\lambda _{\gamma }(\sigma l)+\lambda _{\gamma }(\sigma ^{'}l+1)\right)\left[1+\alpha _{KW}(\sigma l+\sigma ^{'}l+1)\right]=\lambda _{\gamma }(\sigma l)[1+\delta _{\gamma }^{2}][1+\alpha _{KW}]={{1} \over {\tau }}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77545480b7131a0689d3577dc36b4ee8af429c0d)
Jeśli wykorzystamy definicję średniego czasu rozpadu promieniowania elektromagnetycznego jako odwrotność jego stałej rozpadu, wtedy dla multipolowości σl mamy:

Stała zaniku dla promieniowania o multipolowości σl+1 określamy przy pomocy wzoru (3.91) wiedząc, że mamy stałą zaniku dla multipolowości σl (3.112).

Biorąc zredukowane prawdopodobieństwo rozpadu według wzoru (3.109), to wtedy możemy obliczyć B(σl) i B(σl+1) dla składowych o multipolowościach σl i σ'l+1, które noszą nazwę zredukowanych parcjalnych prawdopodobieństw przejść γ dla składowych σl i σ'l+1.
Konwersja wewnętrzna par e-e+(KWP)[edytuj]
Poznaliśmy już przejścia elektromagnetyczne i konwersję wewnętrzną (KW), które maleją wraz ze wzrostem energii przejścia i rosną ze wzrostem Z jądra, one zachodzą dla energii przejścia ok. 1MeV, współczynnik WKW jest 10-3. Gdy Ei-Ef≥2mec2=1,022MeV przejście dodatkowo może zachodzić z utworzeniem pary e+e-. Para elektron-pozyton unosi energię równą:

Moment pędu pary e+e- jest większy od wartości bezwzględnej różnicy wartości momentów pędu poszczególnych jąder krańcowych (jądro przed i po rozpadzie) i jest natomiast mniejsza od sumy jąder momentów pędu jąder krańcowych, tą zależność piszemy:

Parzystość unoszoną przez parę jest natomiast równa:

Widmo energii e+ i e- jest ciągłe, tzn. energia pary jest od E=0 do Emax=(E_i-E_f)∼ 1,022MeV. Pozytony utworzone w wyniku tego rozpadu anihilują z elektronami ośrodka najczęściej według przemiany poniżej w wyniku czego powstaje kwant γ o energii Eγ=511keV:

Proces KWP nie jest powiązany żadną powłoka elektronową, więc prawdopodobieństwo słabo zależy od liczby atomowej jądra Z (maleje ze wzrostem Z). Zdefiniujmy współczynnik KWP, który jest stosunkiem stałej zaniku z utworzeniem pary i stałej zaniku promieniowania γ:

- rośnie ze wzrostem E przejścia dla E równą od 1,5 do 5MeV αp jest od 10-4 do 10⋅10-4.
- jest funkcją przejścia, tzn. σP(σl)>αP(σl+1) i σP(El)>αP(Ml).
- prawdopodobieństwo KWP silnie zależy od kąta θ między kierunkami wylotu e+ i e-.
Pomiary αp i korelacja kierunków wylotu e+ i e- wykorzystuje się do określenia σl o Eγ≥5MeV. Obliczenie teoretyczne αl są trudne do wykonania, ponieważ to wymaga znajomości funkcji falowej jądra i pary e+ i e-.
Rozczepienie spontaniczne (spontanic fission(sf))[edytuj]
W tym rozkładzie ciężkie jądro dzieli się spontanicznie na dwa fragmenty z emisją kilku neutronów:

Energia rozszczepienia jest różnica masy jądra przed rozszczepieniem i sumy mas jąder po rozszczepieniu i masy ν neutronów:
![{\displaystyle Q_{sf}(A,Z)=[M_{j}(A,Z)-(M_{j}(A,Z_{1})+M_{j}(A_{2},Z_{2})+\nu m_{n})]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/080e0826611dcc664fc423eb5718ac4acc2b45dc)
Aby rozszczepienie nastąpiło, to energia Qsf powinna być większe niż zero, co jest spełnione tylko dla jąder ciężkich na opadającej części wykresu B/A. Jeśli dodatkowo założymy, że Bj=E(A,Z)⋅A, to otrzymamy inny ale równoważny do (3.119) używając tylko energii wiązań przypadającej na jeden nukleon.
 gdzie:
gdzie: 
Patrząc na wzór (3.121), aby zachodził warunek Qsf(A,Z)>0, to musi być spełniony 

Fragmemty rozszczepienia, czyli jądra wzbudzone z nadmiarem n ulegają
- rozpadowi β-
- deeskcytacji stanów F* w wyniku przejść EM(γ) lub emisję neutronów przez jądro.
Widmo fragmentów jądra rozszczepiającego się w wyniku rozpadu (3.119) jest dwugarbne, jeśli jądro rozpada się bez emisji neutronów, tzn. spełnione są warunki:


Mechanizm sf[edytuj]
Rozpatrzmy mechanizm rozszczepienia sf bez emisji neutronów na dwa fragmenty, dla którego zachodzą warunki (3.123) i (3.124), wtedy rozszczepienie wygląda:
 gdzie:
gdzie:  i
i  oraz
oraz  i
i 
Energię jądra będziemy określać według modelu kroplowego (1.31). Załóżmy, że podział jądra zachodzi przez podział jądra na dwa sferyczne fragmenty, wtedy energia wydzielająca się w wyniku rozczepienia jest:
![{\displaystyle Q_{sf}(X)=[E_{s}(X)+E_{C}(x)]-[\underbrace {E_{s}(F_{1})+E_{s}(F_{2})} _{1,25E_{S}(X)}+\underbrace {E_{C}(F_{1}(F_{1})+F_{C}(F_{2})} _{0,64E_{C}(X)}]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e85d949ecf3f649e4ff3fe11ba44fd10212c79d)
We wzorze (3.116) energię oznaczoną przez wskaźnik S oznacza efekty powierzchniowe, które pozwalają utrzymać kształt sferyczny jądra, a przez wskaźnik C będziemy oznaczać jako oddziaływanie kulombowskie, które starają się rozerwać jądro. W mechanizmie sf istotną rolę odgrywają energie EC i ES. stąd energię jądra (3.116) możemy przepisać:

Można pokazać wykorzystując relację na energię wiązania w modelu kroplowym, że dla Qsf(X)>0, gdy Z2/A>17. Jądra spełniające ten warunek mogą ulec natychmiastowego rozszczepieniu z czasem połowicznego zaniku T1/2≈10-22s. Dla A=2Z otrzymamy natychmiast Z>34, czyli dla tych jąder następuje rozszczepienie. Doświadczalnie stwierdzono, że sf występuje tylko w jądrach ciężkich dla Z≥90 i zachodzi z bardzo małym prawdopodobieństwem, bo np. czas połowicznego rozpadu dla tego jądra uranu 238 jest 

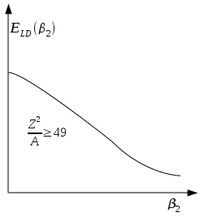
Funkcja (3.121) rośnie przy wzroście β2, więc to pełni rolę bariery energetycznej ΔEsf przy podziale jądra. Dla małych β2 przy energii jądra niezdeformowanego ELD(Z,A,0) energię jądra zdeformowanego piszemy poprzez:

Jeśli (2Es-EC<0, to ELD(β2) jest funkcją malejącą, wtedy nie ma bariery na rozczepienie. Warunek ten jest spełniony dla Z2/A≥49, gdy Z≥120, wtedy rozpad sf jądra jest natychmiastowy, wtedy czas połowicznego zaniku jest rzędu 10-22s. Jeżeli (2Es-EC)>0 bariera występuje, a jej wysokość maleje w miarę zmniejszania się parametru Z2/A≤49, wtedy sf zachodzi tylko w wyniku przejść tunelowych, i czas połowicznego zaniku silnie zależy od Z2/A. Przy większej deformacji prowadzącej do rozszczepienia jądra atomowego poprawki powłokowe zakładające gładką zależność bariery na rozczepienie mogą prowadzić do pojawienia się drugiego minimum. Tłumaczy to zjawisko izometrii rozszczepieniowej. Ze względu na rozczepienie bariery połowiczny czas życia stanu podstawowego jest większy lub równy czasowi stanu izomerycznego, tzn.T1/2(sf)st. podst.≥T1/2(sf)st. izomer., dla jądra 238U mamy czas zycia poziomu podstawowego T1/2≈6⋅1015lat, a czas życia poziomu izomerycznego jest T1/2≈195⋅10-9s. Uwzględnienie δEshell+δEparing, czyli energię uwzględniające strukturę powłokową jądra i energię parowania, pozwalają dokładnie opisać wysokość bariery na rozszczepienie w poszczególnych jądrach oraz obserwowaną doświadczalnie silną zależność sf od struktury jądra atomowego, i pozwalają zrozumieć dwugarbny charakterystyczny rozkład mas w wyniku rozczepienia jądra atomowego w rozczepieniu asymetrycznym.