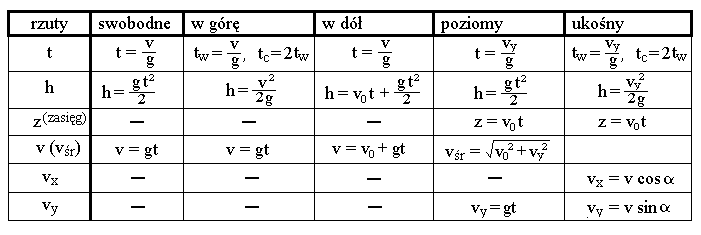Fizyka dla liceum/Rzuty

Rzuty

Wstęp

Przyspieszenie ziemskie
Siła grawitacji powoduje, że każde rzucone ciało (takie tu będziemy rozpatrywać) posiada przyspieszenie, zwane przyspieszeniem ziemskim g, skierowane pionowo w dół. Jego wartość jest umowna, ponieważ w różnych miejscach Ziemi jest ona inna - grawitacja planety nie jest jednorodna.

Jeśli jednak wszystkie ciała spadają z tym samym przyspieszeniem, interesujące może być pytanie, dlaczego człowiek ze spadochronem spada wolniej od osoby bez spadochronu? Przyspieszenie jest stałe, jednak na prędkość wpływają również opory powietrza. Duża powierzchnia ciała skutkuje większym oporem, a ciało 'opada' wolniej. Fakt ten nie był dostrzegany przez ludzi aż do odkrywczych doświadczeń Galileusza w XVII wieku.

przyspieszenie ziemskie:

g = 9,81 m/s²

Spadek swobodny
Spadek ciała możemy opisać jako ruch przyspieszony. Wartość przyspieszenia jest równa przyspieszeniu ziemskiemu: a = g. Drogę przebytą przez ciało, dla ułatwienia, możemy nazywać wysokością (h) z jakiej ciało spadło: s = h. Prędkość wyraża się wzorem z ruchu przyspieszonego v=at.

Aby obliczyć, z jakiej wysokości spadło ciało, wystarczy zmierzyć czas jego upadku. Natomiast w celu obliczenia czasu upadku - postąpimy na odwrót. Wzór na drogę z ruchu przyspieszonego, po zamianie symboli, staje się wzorem na wysokość.

(przypominamy wzór na drogę)   $s={\frac {\,at^{2}}{2}}$

wysokość początkowa  $H={\frac {\,gt^{2}}{2}}$

Wysokość w pewnej chwili t₁ liczymy inaczej. Słownie jest to: przebyta droga odjęta od wysokości początkowej, po przełożeniu na wzór:

położenie w pewnej chwili t₁:  $h=H-{\frac {\,gt_{1}^{\;2}}{2}}$

Rzut pionowy

Rzut w dół

Rzut pionowy w dół można kojarzyć ze spadkiem swobodnym. Różni się jednak od niego, ponieważ ciało rzucone ma swoją prędkość początkową. Podobnie jak w ruchu przyspieszonym, gdzie prędkość początkowa wpływała na drogę, w ten sam sposób dodajemy ją do wzoru na wysokość. Wzór na wysokość:

wysokość początkowa $H=v_{0}t+{\frac {gt^{2}}{2}}$

(v₀ -prędkość z jaką rzucono ciało, t - czas spadania)

Wysokość w danej chwili t₁, analogicznie jak przy opisie spadku swobodnego, opisana jest wzorem "h = wysokość - przebyta droga". Jak pamiętamy, przebyta droga liczona jest jako: $v_{0}t+{\frac {\,gt_{1}^{\;2}}{2}}$.

Prędkość ciała — przypomnijmy ruch przyspieszony — jest to: v = v₀ + at.

Rzut w górę

Prześledźmy jak zachowuje się ciało rzucone pionowo w górę. Z początkową prędkością leci ku górze, jednak z czasem wyhamowuje, z powodu przyspieszenia ziemskiego (skierowanego w dół). Osiąga pewien punkt i zatrzymuje się, na maksymalnej wysokości h_max. Przyspieszenie nadal wpływa na ciało, więc zaczyna nabierać prędkości lecąc w dół - jak w ruchu przyspieszonym.

Ruch pionowo w górę przebiega jak ruch opóźniony, który dobrze znamy i potrafimy opisać, obliczymy dzięki temu wysokość - bo jest ona równa drodze, którą ciało przebywa podczas ruchu (w czasie t lotu ku górze).

(droga w ruchu opóźnionym)  $s=v_{0}t+{\frac {-at^{2}}{2}}$

wysokość początkowa  $H=v_{0}t+{\frac {-gt^{2}}{2}}$

Zauważmy, że musi być minus przy przyspieszeniu g, ponieważ jest przeciwnie skierowane (w dół) niż kierunek lotu ciała (w górę!). Gdybyśmy go pominęli, byłby to wzór dla ruchu przyspieszonego (ciało przyspieszałoby lecąc do góry).

Przypomnijmy jak obliczamy prędkość w danej chwili w ruchu opóźnionym:   $v=v_{0}-at\,$

Jak znajdziemy czas wznoszenia się ciała? Podobnie jak liczyliśmy czas końca ruchu opóźnionego, kiedy v=0, policzymy czas wznoszenia, czyli z przekształconego wzoru na prędkość.

$t_{w}={\frac {v_{0}}{g}}\qquad -$  ze wzoru na prędkość, po podstawieniu v=0 (prędkość końcowa gdy ciało się zatrzymało)

Wysokość maksymalną można więc obliczyć bez czasu wznoszenia — podstawiając za niego powyższy wzór, otrzymamy drugą wersję wzoru na wysokość, wysokość maksymalną:

$h_{max}={\frac {v_{0}^{\,2}}{2g}}$

Ciało po osiągnięciu maksymalnej wysokości zaczyna lecieć w dół, co przebiega jak w upadku swobodnym. Całkowity czas  t_c  jest dwa razy większy niż czas wznoszenia:

czas całkowity   $t_{c}={\frac {2v_{0}}{g}}$

Rozpatrzmy kilka sytuacji pewnego rzutu w górę: początek ruchu, jego środek (gdy osiąga maksymalną wysokość) oraz koniec (upadek). Prześledźmy po kolei te etapy.
Wzór na prędkość:  $v\,=v_{0}-gt$

1. Początek t=0:   $v\,=v_{0}-0\;\rightarrow \;v=v_{0}$

prędkość ciała to prędkość nadana przy rzucie

2. Zatrzymanie się, t=t_w:   $v\,=v_{0}-gt_{w},\quad t_{w}\,={\frac {v_{0}}{g}}$

$v\,=v_{0}-g{\frac {v_{0}}{g}}\;\rightarrow \;v=0$

ciało osiąga maksymalną wysokość, zatrzymuje się, prędkość równa zero; zaczyna upadać

3. Moment upadku t=t _c:   $v=v_{0}-gt_{c}\;\rightarrow \;v=v_{0}-g\cdot 2t_{w},\quad t_{w}\,={\frac {v_{0}}{g}}$

$\;\rightarrow \;v=v_{0}-2v_{0}\;\rightarrow \;v=-v_{0}$

Okazuje się, że ciało w momencie upadku porusza się z prędkością v = -v₀.  Oznacza to, że wartość prędkości końcowej jest równa wartości prędkości początkowej, ale ich zwroty są przeciwne, na co wskazuje minus. Prędkość końcowa jest skierowana w dół, czyli ma zwrot zgodny z przyspieszeniem ziemskim - ruch w dół jest przyspieszony (tak jak zakładaliśmy).

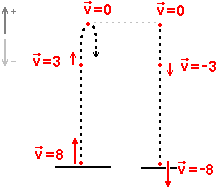
Obok rysunek przedstawiający przykładową sytuację. Ciało zostaje rzucone z prędkością v=8. Porusza się w górę, z każdą sekundą tracąc prędkość, aż do zatrzymania, po czym zaczyna swobodnie spadać w dół (prędkości o przeciwnym zwrocie są ujemne). Oczywiście, torem ruchu jest pionowa linia w górę (rysunek dla przejrzystości jest trochę zakłamany).

Rzut w górę - podsumowanie

Ciało otrzymuje prędkość początkową. Ruch odbywa się w górę (wznoszenie) oraz w dół (opadanie), oba są przy udziale przyspieszenia ziemskiego.

Prędkość ciała w dowolnej chwili wynosi ${\vec {v}}={\vec {v}}_{0}+{\vec {g}}t$, a po uwzględnieniu przeciwnych zwrotów (prędkość w górę, przyspieszenie w dół): $v=v_{0}-gt$.

W pewnym momencie v zacznie przyjmować wartości ujemne. Rozumiemy przez to, że początkowo obrany kierunek ruchu zmienił się na przeciwny.

Wysokość maksymalna: liczona jest jak droga w ruchu opóźnionym, czyli   $h_{max}=v_{0}t+{\frac {(-g)t^{2}}{2}}\,$.

Rzut poziomy

Załóżmy, że mamy ciało na pewnej wysokości. Nadajemy mu prędkość w kierunku poziomym. Jednocześnie, przyspieszenie ziemskie powoduje ruch ciała w dół. Musimy więc złożyć oba ruchy, aby znaleźć, jak ostatecznie będzie się poruszało.

Ciało posiada prędkość v₀ w kierunku poziomym oraz przyspieszenie g skierowane w dół, które jest przyczyną ruchu przyspieszonego w dół z rosnącą prędkością v_y (od współrzędnej wysokości: y). Użyliśmy oznaczeń: prędkość pionowa v_y, prędkość pozioma początkowa v₀. Prędkość wypadkowa jest sumą wektorów obu tych prędkości, i nadaje ona ostateczny kształt ruchu.

Jak będzie poruszać się ciało? Wydawałoby się, że po ukosie, jednak tor będzie zbliżony do łuku, który coraz silniej wędruje ku dołowi. Będzie tak ponieważ prędkość v_y spadania rośnie w każdej sekundzie o g (ruch przyspieszony), przez co ciało coraz silniej opada w dół; natomiast prędkość pozioma v₀ nie zmienia się.

Co ciekawe, prędkość wypadkowa nie jest nam potrzebna. Na wysokość wpływa tylko prędkość v_y, natomiast na zasięg (odległość) wpływa wyłącznie prędkość v₀.

Drogę przebytą przez ciało rozpatrzymy w obu wymiarach osobno - przebyta wysokość oraz zasięg rzutu.

Poslugując się równaniem drogi dla ruchu przyspieszonego obliczmy, na jakiej wysokości znajduje się ciało w chwili t:

droga (ruch przyspieszony):   $s={\frac {at^{2}}{2}}$

wysokość w chwili t: $h=H-{\frac {gt^{2}}{2}}$

(wysokość = wysokość początkowa - przebyta droga)

Zasięg, czyli odległość przebytą w poziomie, obliczymy z równania na drogę w ruchu jednostajnym, ponieważ ciało w kierunku poziomym porusza się ze stałą prędkością v₀.

$z\,=v_{0}t$

Jeśli nie mamy podanego czasu upadku, możemy obliczyć zasięg podstawiając $t={\sqrt {\frac {2H}{g}}}$

Rzut ukośny

Ciało porusza się z prędkością, której wektor skierowany jest ukośnie - pod kątem alfa do poziomu. Prędkość możemy rozłożyć na dwie składowe - pionową i poziomą (analogia do dodawania wektorów). Tak więc prędkość ukośna v₀ to inaczej prędkości składowe: v_0x oraz v_0y (rzuty v₀ na osie układu współrzędnych).

Wartości wektorów składowych można obliczyć z funkcji trygonometrycznych. Jeżeli znamy kąt, jaki tworzy nasz wektor prędkości, umiemy wyznaczyć składowe v_x i v_y:

$v_{0x}\,=v_{0}\,\cos {\alpha }$

$v_{0y}\,=v_{0}\,\sin {\alpha }$

Możemy już mówić o dwóch ruchach ciała. Ruch poziomy, jednostajny - bez przyspieszenia, z nadaną prędkością v_0x. Położenie, odległość ciała w danej chwili, możemy kojarzyć z drogą w ruchu jednostajnym (oznaczmy je x). Wzór na drogę s=vt.

$x\,=v_{0x}\,t$

Ruch w kierunku pionowym to ruch opóźniony, z przyspieszeniem ziemskim zwróconym ku Ziemi. Prędkość v_0y skierowana w górę, 'spowalniana' przez przyspieszenie - sytuacja jak w rzucie pionowym. Położenie w linii pionowej, czyli wysokość, obliczymy jak drogę w ruchu opóźnionym.

$y\,=v_{0y}\,t-{\frac {gt^{2}}{2}}$

Równanie toru
Jeśli podstawimy w powyższych równania wzory na odpowiednie prędkości, uzyskamy
$x\,=v_{0}\,\cos {\alpha }\cdot t\qquad y\,=v_{0}\,\sin {\alpha }\cdot t-{\frac {gt^{2}}{2}}$
Wyznaczając czas t z równania x i podstawiając do równania y, otrzymamy równanie toru:

$y\,={\mbox{tg}}\alpha \,x-{\frac {gx^{2}}{2v_{0}^{\,2}\cos ^{2}\alpha }}$

Dzięki temu równaniu możemy narysować w układzie współrzędnych tor lotu (jest to równanie paraboli) i wyznaczyć inne wzory. Równanie to pokazuje zależność pomiędzy wysokością a odległością od punktu wyrzutu (o ile znamy prędkość początkową i kąt wyrzutu).

Aby wyznaczyć zasięg rzutu (maksymalną odległość), należy sobie uświadomić, że ciało znajdzie się najdalej, gdy będzie na wysokości 0. W równaniu toru za y podstawimy 0; po przekształceniach otrzymamy:

$z\,={\frac {v_{0}^{\,2}\sin {2\alpha }}{g}}$

Czas całkowity, czyli czas wznoszenia i opadania razem wzięte:

$t_{c}={\frac {2\cdot v_{y}}{g}}$

Co można rozwinąć do:

$t_{c}\,={\frac {2v_{0}\sin \alpha }{g}}$

Maksymalną wysokość otrzymamy, gdy do równania na y podstawimy połowę czasu całkowitego $t_{c}\,$ (czyli $t_{w}\,$, czas wzlatywania, wtedy wysokość jest największa). Po przekształceniach otrzymamy:

$H_{max}\,={\frac {v_{0}^{2}\sin ^{2}\alpha }{2g}}$

Tabelka podsumowująca

Zadania

Zad. 1 (rzut ukośny) Strzelamy pociskiem tak, aby trafić przedmiot znajdujący się na wysokości h₀ i w odległości d. Przedmiot w momencie wystrzału spada swobodnie w dół. Pod jakim kątem należy strzelić, aby pocisk trafił przedmiot?

(W rozważaniach pomijamy opór powietrza. Dlatego też w rzeczywistości sytuacja może wyglądać trochę inaczej)

Warunkiem zadania jest, aby pocisk trafił spadający przedmiot, wnioskujemy stąd, że ich wysokości muszą być równe (w momencie zderzenia), zapiszmy:

w momencie t mamy:

położenie Y pocisku   $y=v_{0}t\sin {\alpha }-{\frac {gt^{2}}{2}}\qquad -$ z podstawieniem v_0y

położenie Y przedmiotu   $y=h_{0}-{\frac {gt^{2}}{2}}\qquad -$ upadek swobodny

z powyższych mamy: $v_{0}t\sin {\alpha }-{\frac {gt^{2}}{2}}=h_{0}-{\frac {gt^{2}}{2}}$

Opiszemy jeszcze równanie położenia poziomego:

położenie X pocisku   $x\,=v_{0}t\cos {\alpha }$

W obu równaniach mamy nieznany czas t, pozbędziemy się go z równań poprzez podstawienie. Wyznaczymy t z równania na Y i podstawimy do równania na X.

wyznaczamy czas   $t={\frac {h_{0}}{v_{0}\sin {\alpha }}}$

podstawiamy  $x\,=v_{0}{\frac {h_{0}\cos {\alpha }}{v_{0}\sin {\alpha }}}\quad \rightarrow \quad tg\,\alpha \,={\frac {h_{0}}{x}}$

Wzór ten skojarzmy z wzorem na tangens w trójkącie prostokątnym. Jeśli narysujemy ten trójkat z kątem alfa, bokami h₀ oraz x w odpowiednich miejscach, będzie to rysunek przedstawiający sytuację z zadania - pocisk jest wystrzelony w 'kierunku przedmiotu'. Innymi słowami, strzelamy dokładnie pod kątem, pod jakim cel jest widoczny (bez żadnego "zapasu")- taka również jest odpowiedź.

Dodatkową, ciekawą obserwacją jest, że przyspieszenie ziemskie, fakt spadania kuli, czy nawet prędkość pocisku, nie wpływa na zmianę kąta, pod którym strzelamy. Jak to jest, że nie trzeba brać żadnych poprawek na kąt wystrzału, mimo że kula swobodnie spada? Spowodowane to jest tym, że pocisk i kula spadają w dół takim samym ruchem (przyspieszonym). Każdy ruch kuli w dół jest "równoważony" przez wyhamowywanie pocisku (który też jest przyciągany w dół). Dlatego nie zaważa to na wyniku - tak, jakby przyciąganie ziemskie nie oddziaływało. W rzeczywistości jednak dochodzą inne siły, których tu nie braliśmy pod uwagę, np. opór powietrza, powierzchnia przedmiotów itd.

---