Liczby zespolone/Wersja do druku

| ||
Spis treści[edytuj]
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
(...)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Zobacz też[edytuj]
Historia liczb zespolonych[edytuj]
Historia liczb zespolonych sięga już tysięcy lat. Już sam wielki Heron z Aleksandrii (10-70), znany nam m.in. ze wzoru umożliwiającego obliczenie pola powierzchni trójkąta ze znajomości wymiarów jego boków, konstruując opisy matematyczne służące do wyznaczania pól podstaw, objętości i mas budowanych piramid, zastanawiał się nad równaniami kwadratowymi. Z pozoru były proste w obliczeniach, jednak ich rozwiązania nie zawsze mieściły się w ówcześnie poznawanej przestrzeni liczb rzeczywistych.
Spróbujmy teraz sami przyjrzeć się chociażby prostemu równaniu:
Co stałoby się jeśli liczba s stałaby się ujemna (-s) i z kolei a,b,c pozostały dodatnie?
Po chwili na pewno każdy z was zauważy, że w tym dziwnym układzie, pomimo wprowadzenia znaku ujemnego – po wyciągnięciu znaku przed nawias - pierwiastek wciąż pozostanie dodatni i będziemy mogli znaleźć wartość liczby P:
Jednak od razu nasuwa się nam myśl, że przecież - co widać gołym okiem - pierwiastkujemy liczby ujemne:
a takie działania przecież, według szkolnej nauki, nie przynoszą nam skutku.
Jednak ludzkość, szczególnie jej część europejska, przez kolejne wieki nie zainteresowała się rozwikłaniem jakichkolwiek rozważań w tej dziedzinie, uznając je najprawdopodobniej za niekonwencjonalne i, zamiast drapać się w głowę, wolała skupić się na wegetatywnym wykorzystaniu dotychczasowych osiągnięć matematyki - ze względów ideologicznych ignorując istnienie liczb choćby ujemnych.
Prawdziwe odrodzenie w matematyce przyniósł XVI wiek. Oprócz mnóstwa nagromadzonych przez lat pytań, znalazło się wielu śmiałków, którzy ochoczo starali się na nie odpowiadać. Jednym z nich był włoski matematyk Girolamo Cardano (1501-1576). W roku 1545 sporządził on dzieło Ars Magna (Wielka Sztuka), w którym rozważył taki oto problem:
- „Gdyby ktoś kazał Tobie wziąć liczbę 10 i podzielić ją na dwie części, tak by pomnożone jedna z drugą dały 40 – odpowiesz niemożliwe. Jednak rozwiążemy to równanie dla Ciebie”
- Rozpiszmy więc układ równań:
- otrzymamy zeń równanie kwadratowe:
- do którego rozwiązania wyznaczymy z definicji deltę ,
- oraz nie przejmując się ujemnością delty, wyznaczymy pierwiastki równania oraz będące rozwiązaniami problemu!
Problem ten nie definiował liczb zespolonych jako takich, ale jego rozwiązanie wynikało z zastosowania własności tych liczb. Cardano posunął się dalej w rozważaniach, używając prywatnych i niepublikowanych wcześniej prac Niccolò Tartaglii (1500 - 1556) - który jako pierwszy rozwiązał równania trzeciego stopnia. Ich twierdzenia były dla ówczesnych matematyków rodzajem herezji - w końcu nie dość, że swobodnie używali oni liczb ujemnych, to mieli czelność je pierwiastkować.
Przełomu dokonał dopiero trzydzieści lat później, uważany za "ojca liczb zespolonych", Rafael Bombelli (1526-1572). Nie był on matematykiem, lecz zwykłym inżynierem, zajmującym się m.in. hydrologią. Nie przejmując się twierdzeniami środowiska matematycznego, zaprzeczającego istnieniu pierwiastka liczb ujemnych - po prostu go zastosował. René Descartes nazywał taki pierwiastek przewrotnie liczbą wyimaginowaną (urojoną).
Zwolennicy liczb urojonych z czasem poczęli oznaczać pierwiastek z -1 literką i (z łac. imaginarius), przyjmując że . Zwyczaj ten rozpropagował Euler.
Definicje, twierdzenia, wzory[edytuj]
Dla lepszego ogarnięcia wiedzy zakresu liczb zespolonych, warto sobie przypomnieć jakie w ogóle mamy podstawowe zbiory liczbowe i ich oznaczenia:
- - zbiór liczb naturalnych (z ang. natural, naturalny),
- - zbiór liczb całkowitych (z niem. Zahlen, liczby),
- - zbiór liczb wymiernych (z ang. quotient, iloraz),
- - zbiór liczb niewymiernych,
- - zbiór liczb rzeczywistych (z ang. real, rzeczywisty),
- oraz nowo poznawany – - zbiór liczb zespolonych (z ang. complex, złożenie),
W algebrze pojęcie liczb stale się zmieniało, a znane zbiory liczbowe ulegały nieustannemu poszerzaniu. Nowe pojęcia liczb wprowadzano zawsze wtedy, kiedy wyniki zasadniczych działań nie mieściły się w dotychczasowych zbiorach liczbowych. Stąd też odejmowanie liczb naturalnych większych od mniejszych wprowadziło z czasem nieuniknioną konieczność utworzenia liczb ujemnych. Z połączenia obu tych zbiorów powstał zbiór liczb całkowitych. Jednak i tu, ze względu na dzielenie, a dokładnie niepodzielność niektórych liczb całkowitych względem siebie, należało wprowadzić obok liczb wymiernych zapisywanych jako ułamki - liczby niewymierne, których dokładnego wymiaru nie jesteśmy w stanie zapisać w ułamku. Liczby niewymierne dopełniły więc poprzedni zbiór liczb wymiernych, tworząc w połączeniu przestrzeń liczb rzeczywistych, którą można łatwo zobrazować, np. na osi współrzędnych:

W rozdziale historia zwróciliśmy uwagę, że również w przypadku tak zaawansowanego zbioru liczb jakim jest zbiór rzeczywisty, mamy problem z określeniem wartości pierwiastka kwadratowego z liczb ujemnych. Wykraczają one bowiem poza zakres tego zbioru – znajdują się poza nim. Stąd istniała konieczność powołania przestrzeni, w której zawierałaby się zarówno przestrzeń liczb rzeczywistych oraz przestrzeń zawierająca pierwiastki z liczb ujemnych. Tą potrzebną przestrzenią stały się liczby wyimaginowane (urojone) - z łaciny oznaczane Im lub (łac. imaginarius).

W roku 1673, angielski matematyk, John Wallis (1616 - 1703) stwierdził, że liczby urojone nie mieszczą się na osi liczb rzeczywistych lecz wokół niej, co łatwo zobrazowaliśmy sobie na powyższym rysunku.
Liczby urojone, jak więc widać, są dopełnieniem zbioru liczb rzeczywistych - w połączeniu z którym tworzą zbiór liczb zespolonych .

Posiadając już tego typu wstępne wiadomości, z powodzeniem możemy zagłębić się w świat matematyki i przedstawić sobie kilka kolejnych definicji, twierdzeń i wzorów poruszonych w kolejnych podrozdziałach.
Liczby urojone[edytuj]
| Pierwiastek kwadratowy liczby ujemnej, , nazywamy liczbą urojoną (liczbą wyimaginowaną - Imaginarius). |
Pomysł o istnieniu liczby ujemnej, jest niemal czysto filozoficzny. Skoro na świecie miałyby istnieć liczby dodatnie, to zapewne musiałyby istnieć liczby do nich przeciwne. Tylko jak współdziałałyby one ze sobą?
Znany nam z historii Rafael Bombelli bardzo interesował się matematyką. W swoim dziele "Algebra", opublikowanym w roku 1572, zauważył ciekawą rzecz znamienną dla liczb rzeczywistych, którą warto tutaj sobie przypomnieć. Określił on bowiem działania na liczbach rzeczywistych w zależności od znaku liczby - co można w skrócie zapisać:
- dodatnia razy dodatnia, daje dodatnią
- ujemna razy ujemna, daje dodatnią
- dodatnia razy ujemna, daje ujemną
- ujemna razy dodatnia, daje ujemną
Skoro tak to można byłoby zadać sobie pytanie - czy istnieją jakieś liczby, które przy zastosowaniu tych samych zasad dawałyby wynik zupełnie przeciwny?
Określenie działań na liczbach ujemnych było wprowadzeniem niezbędnym do poznania sposobów zachowania się ich pierwiastków, Bombelli określił bowiem zachowanie się pierwiastków liczb ujemnych w oparciu o powyższą zasadę. W swojej książce napisał, że:
czyli słownie:
- dodatni pierwiastek liczby ujemnej razy dodatni pierwiastek liczby ujemnej, daje liczbę ujemną
- ujemny pierwiastek liczby ujemnej razy ujemny pierwiastek liczby ujemnej, daje liczbę ujemną
- dodatni pierwiastek liczby ujemnej razy ujemny pierwiastek liczby ujemnej, daje liczbę dodatnią
- ujemny pierwiastek liczby ujemnej razy dodatni pierwiastek liczby ujemnej, daje liczbę dodatnią
Jak widać, liczby urojone poddawały się tym samym własnościom, co liczby rzeczywiste, ale z różnicą wyniku (co do znaku) - co może się nam teraz wydawać niemal zupełnie oczywiste. Skoro jednak liczby urojone otrzymujemy na podstawie różnych konfiguracji działań na liczbach rzeczywistych, to czemu miałoby być też inaczej - wystarczy przemnożyć by sprawdzić. Dla ówczesnych matematyków jednak to takie proste nie było. Przy takim nowym zapisie musieliby oni uznać, często wcześniej pomijany fakt, że pierwiastek kwadratowy liczb rzeczywistych jest funkcją dwuwartościową, np. ale też .
Wynikałoby stąd, że działania na liczbach urojonych zachowują kształt działań jak przy liczbach rzeczywistych. Stąd też, zbiór liczb urojonych nazywa się izomorficznym (równokształtnym) ze zbiorem liczb rzeczywistych. Jednak w tym momencie samą ideologią tego słowa nie warto zaprzątać sobie głowy - są ważniejsze problemy.
Niestety, jak powiedzieliśmy sobie wcześniej, wciąż istniały kłopoty z określeniem położenia liczb urojonych względem liczb rzeczywistych. Nasze rysunki poglądowe z poprzedniego rozdziału wybiegały daleko w przyszłość. Do tego, w międzyczasie doszedł jeszcze problem niewygodnej i zawiłej notacji. Przez kolejne lata, przy rozwiązywaniu równań kwadratowych, jak i wyższego rzędu, wciąż stosowano dla miejsc zerowych zapis typu: . Już sam pierwiastek nie wygląda przystępnie i wzbudza zmieszanie wśród ludzi znających podstawowe prawa arytmetyki - głoszące brak rozwiązania takiego działania - a co dopiero, jeśli taki pierwiastek napiszemy w złożeniu z inną liczbą.
W roku 1777 przyszedł z pomocą szwajcarski matematyk Leonard Euler. Zaproponował on dość banalny sposób rozwiązania problemów, jakie stwarza widok pierwiastka liczby ujemnej. Dla przykładu - dysponując liczbą , zawsze przecież, możemy wyciągnąć z niej część rzeczywistą prostym działaniem matematycznym:
Jak więc widać, w zasadzie każda liczba urojona może zostać zapisana w takiej postaci - bo dla każdej liczby rzeczywistej u oraz odpowiedniej rzeczywistej b możemy napisać: , oraz:
Euler zaproponował, aby zamiast pisać po prostu . W końcu, skoro możemy pisać ° jako oznaczenie stopnia kąta - to czemu nie użyć literki i jako symbolu imaginacji - urojenia.
Stąd też założenie, że litera i oznacza jednostkę urojoną wynoszącą pierwiastek z minus jeden[1]
Dzięki temu, liczby urojone możemy zapisywać w wygodnej, nie budzącej już grozy, postaci , gdzie jest jakąś liczbą rzeczywistą powstałą jak powyżej.
Jednak założenie to było niewystarczające (jak objaśniono w przypisach) dlatego też bazując na zdobytych wcześniej doświadczeniach lepiej było założyć:
- ↑ Sprawa wyjaśniania notacji jest wciąż dyskusyjna i może początkowo sprawiać kłopot w zrozumieniu.
to umowne oznaczenie jednostki urojonej, dzięki któremu możemy zapisać liczby urojone w postaci bi.
Jednak wprawne oko zauważy, że analizując pewne działania możemy otrzymać ciekawą formę:
Dlatego by wykluczyć wątpliwości, idąc dalej, należy przyjąć, że najpierw wykonujemy operacje na wykładnikach potęgi:- skoro to zapisujemy, że
Płaszczyzna zespolona[edytuj]
Euler wprowadzając swoją notację dla liczb urojonych , z użyciem jednostki urojonej i, znacznie ułatwił analityczny pogląd na ich sprawę. Niestety nadal istniał problem określenia położenia liczb urojonych względem osi współrzędnych liczb rzeczywistych. Matematycy szybko zadali sobie pytanie, gdzie je umiejscowić, jak opisać graficznie.

W roku 1797 norwesko-duński mierniczy Caspar Wessel, w 1799 niemiecki matematyk Carl Friedrich Gauss, oraz w 1809 szwajcarski księgarz Jean-Robert Argand niezależnie wpadli na pomysł geometrycznego przedstawienia tychże liczb - liczb, które nie mieściły się już na całkowicie zajętej osi liczb rzeczywistych (pamiętacie rysunek poglądowy z początku rozdziału?).
Dla przypomnienia powiedzmy, że równania kwadratowe rozpatrywane są w układzie współrzędnych kartezjańskich (), utworzonym przez dwie prostopadłe do siebie osie rzeczywiste - oś Ox (odciętych) oraz oś Oy (rzędnych). Jeśli liczby rzeczywiste rozpatrzymy sobie jako pewną płaszczyznę, rozpiętą pomiędzy dwiema osiami rzeczywistymi to liczby urojone również w tym przypadku powinny leżeć poza obiema osiami - oraz poza tą płaszczyzną.
Spójrzmy na konstrukcję osi liczbowej: mamy pewną wspólną dla wszystkich liczb jednostkę, z pomocą której wielokrotności możemy opisać resztę liczb i równomiernie rozłożyć na linii ciągłej. Dla liczb rzeczywistych taką jednostką, będzie liczba 1 - każda liczba rzeczywista a może być rozpisana jako pewna wielokrotność jedynki. Podobnie mamy z liczbami urojonymi - ich jednostką jest liczba i, a oś tworzona jest identycznie - przez przemnożenie kolejnych liczb rzeczywistych przez jednostkę i.
Szybko możemy zauważyć, że liczby czysto urojone posiadają więc jeden wspólny punkt z osią - w końcu określone są przy użyciu rzeczywistej liczby b. Punktem tym jest 0 (co by nie było 0 razy liczba daje nam zero, zarówno w przypadku liczb rzeczywistych, jak i liczby i). Do osi reprezentującej liczby rzeczywiste - określonej od tej pory symbolem Re (z łac. Realis), należało więc dołączyć oś liczb urojonych - Im (z łac. Imaginarius), zachowując przy tym pewną ogólnie zrozumiałą i akceptowalną konwencję. Skoro już trwaliśmy w układzie kartezjańskim to postanowiono utworzyć coś co będzie go przypominało. Oś urojoną poprowadzono prostopadle do osi rzeczywistej, przecinając ją w zerze (patrz rysunek).
Zabieg przecięcia dwóch osi, w matematyce powoduje rozpięcie pewnej płaszczyzny. Tę płaszczyznę, która zespalała liczby urojone z liczbami rzeczywistymi Gauss nazwał płaszczyzną zespoloną.
| Płaszczyzna zespolona rozpięta jest przeciętymi ze sobą w punkcie (0,0) osiami urojoną Im i osią rzeczywistą Re. |
Stąd nasuwa się prosty pomysł: liczby zawarte w płaszczyźnie zespolonej, prawdopodobnie, powinny być opisane złożeniem liczby rzeczywistej z liczbą urojoną.
Liczby zespolone[edytuj]
| Liczbą zespoloną nazywamy uporządkowaną parę liczb rzeczywistych będących współrzędnymi tej liczby w przestrzeni (płaszczyźnie) liczb zespolonych. |
Ze względu na sposób rozpięcia przestrzeni (płaszczyzny) - liczby zespolone, jak nazwa wskazuje, są złożone: z części określającej położenie na osi rzeczywistej oraz urojonej . W roku 1833 William Hamilton (1805-1865) stwierdził, że skoro liczby rzeczywiste w kartezjańskim układzie współrzędnych można było zapisywać w postaci pary współrzędnych (x,y), to czemu nie zastosować tego sposobu dla liczb zespolonych?
- Stąd powstał:
| Zbiór liczb zespolonych oznaczamy literą : |
Zbiór wszystkich liczb zespolonych będzie więc rozpięty w opisanej wcześniej płaszczyźnie liczb zespolonych, której początkiem jest punkt .
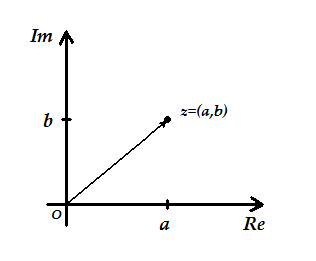
Liczbę zespoloną na płaszczyźnie przedstawia się tak, jak robiło się to z punktami innych układów dwuwymiarowych: w postaci punktu o współrzędnych (a,b) lub w postaci wektora o początku w punkcie O(0,0) i końcu w (a,b).
Jak szybko zauważymy, wszystkie liczby typu będą położone na osi Re - stąd wniosek że możemy je utożsamiać z liczbami rzeczywistymi. Natomiast wszystkie liczby odnajdziemy na osi Im - są liczbami urojonymi.
Mając już zdefiniowaną liczbę zespoloną, warto jest zastanowić się nad własnościami tych liczb. W podręczniku nieustannie powtarzamy, że liczby zespolone to twory matematyczne mające uzupełnić przestrzeń liczb rzeczywistych - toteż poddane różnego rodzaju operacjom powinny się one poniekąd zachowywać podobnie. Toteż poniżej wypisano własności liczb zespolonych.
Własności liczb zespolonych[edytuj]
Dowolne liczby zespolone w określonych przypadkach podstawowych działań matematycznych wykazują własności:
- nie reagują w dodawaniu z zerem:
- ,
- nie reagują w mnożeniu z 1, liczbą :
- ,
- liczba przeciwna do to :
- ,
- przemienność dodawania:
- ,
- łączność dodawania:
- ,
- przemienność mnożenia:
- ,
- łączność mnożenia:
- ,
- rozdzielność mnożenia względem dodawania:
- liczba odwrotna do to :
- ,
Postać algebraiczna[edytuj]
Wróćmy jednak do liczb rzeczywistych i przypomnijmy sobie rozważania na temat pierwiastków liczb ujemnych otrzymywanych przy rozwiązywaniu równań kwadratowych. Liczby te miały nieporęczną postać sumy pewnej liczby rzeczywistej z pierwiastkiem liczby ujemnej.
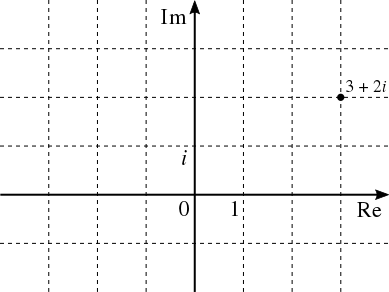
Po wprowadzeniu jednostki urojonej i postać ta stała się bardziej klarowna - jednoznacznie określała bowiem rozdzielność obu typów liczb, w sposób zbliżony do popularnego do dziś sposobu realizacji równań funkcji 2 zmiennych X i Y w układzie kartezjańskim. Szybko zauważymy, że zmieniając wartości rzeczywiste na osi Re, liczba zespolona z na płaszczyźnie przesunie się jedynie w poziomie bez zmian w części urojonej - i na odwrót: zmieniając parametry na osi urojonej Im liczba zespolona przesunie się na wykresie jedynie w pionie, bez zmian części rzeczywistej. Przykładowo jeśli znajdując na osi rzeczywistej liczbę a=3 dodamy do niej liczbę urojoną bi=2i znajdziemy się w punkcie liczby zespolonej o współrzędnych .
Stąd też jeśli a jest częścią rzeczywistą liczby z określoną jako Re(z), oraz b cześcią urojoną liczby zespolonej określaną jako Im(z) to:
- z = Re(z) + Im(z)·i
Każdą liczbę zespoloną można więc przedstawić w postaci algebraicznej:
| liczbę rzeczywistą a nazywamy częścią rzeczywistą liczby zespolonej z, i zapisujemy jako Re(z)=a; liczbę b nazywamy częścią urojoną liczby zespolonej z, i zapisujemy jako Im(z)=b; |
Poprzednią definicję zbioru liczb zespolonych możemy więc rozszerzyć o stwierdzenie że:
| Zbiór liczb zespolonych oznaczamy literą :
|
Obie te postaci są ze sobą równoważne i są ściśle ze sobą związane.
Warto również zauważyć, że liczby postaci lub (0,b), gdzie z pominięciem zera - punktu (0,0), zwykło nazywać się czysto urojonymi (0 jest liczbą rzeczywistą).
Sprzężenie liczby zespolonej[edytuj]
Jakby nie patrzeć, z matematycznego punktu widzenia liczby zespolone są sumą dwóch jednomianów. Element o podwójnej konstrukcji zwany jest w matematyce dwumianem i posiada ciekawą właściwość zwaną sprzężeniem. Liczby zespolone poddają się jego charakterystycznym właściwościom tak samo jak liczby rzeczywiste.
Przypomnijmy sobie definicję tej właściwości:
| Sprzężeniem dwumianu o wyrazach rzeczywistych nazywamy nowy dwumian powstały z wcześniej danego, poprzez wzięcie elementu przeciwnego do drugiego wyrazu tego dwumianu. |

Definicja z pozoru całkiem zagmatwana. Rzeczy najprostsze chyba jest najtrudniej opisać. Kiedy bowiem sobie wszystko rozpiszemy - zabieg wydaje się trywialny.
Sprzężeniem dwumianu rzeczywistego , jest również dwumian rzeczywisty . Jeżeli za y podstawilibyśmy liczbę urojoną, to sprzężenie takie byłoby sprzężeniem liczby zespolonej. Wystarczy tylko spojrzeć na jej postać algebraiczną.
Sprzężenie liczby w matematyce oznacza się na dwa sposoby, albo przez oznaczenie liczby poziomą linią na górze , albo czasami przez oznaczenie liczby tzw. operatorem gwiazdki: .
| Sprzężeniem liczby zespolonej , gdzie nazywamy liczbę opisaną wzorem:
|
.
Spoglądając na wykres, liczba sprzężona do liczby zespolonej jest jej odbiciem w symetrii względem osi rzeczywistej Re.
Właściwości sprzężenia[edytuj]
Sprzężenie dwóch liczb rzeczywistych dawało bardzo przydatną właściwość, znaną ze wzorów skróconego mnożenia. Podobnie jest z liczbami zespolonymi:
- Iloczyn liczby zespolonej i liczby do niej sprzężonej :
- ,
- Sprzężenie liczby sprzężonej:
- ,
- Sprzężenie sumy jest sumą sprzężeń:
- ,
- Sprzężenie różnicy jest różnicą sprzężeń:
- ,
- Sprzężenie iloczynu jest iloczynem sprzężeń:
- ,
- Sprzężenie ilorazu jest ilorazem sprzężeń:
- , zakładając że ,
- Suma liczby zespolonej i liczby do niej sprzężonej :
- Różnica liczby zespolonej i liczby do niej sprzężonej :
- Część rzeczywista sprzężenia:
- ,
- Część urojona sprzężenia:
- ,
Moduł liczby zespolonej[edytuj]
Wartość bezwzględna liczb rzeczywistych była tak zwaną normą - liczbą określającą odległość liczby rzeczywistej od początku układu współrzędnych, bez względu na miejsce, w którym się ta liczba znajdowała. Liczby rzeczywiste przedstawione są na jednej osi - tak więc mogły znajdować się tylko po lewej lub po prawej stronie układu współrzędnych, np. w tej samej odległości = |4| od początku osi liczb rzeczywistych znajdują się dwie liczby: +4 oraz -4.
Nie powinniśmy mieć też problemów z określeniem odległości w przestrzeni liczb zespolonych, które mogą przecież leżeć po bokach osi . O ile tylko potraktujemy jako jednostkę osi urojonej - będziemy mogli rozpatrzyć położenie liczby względem początku nie tylko jednej osi rzeczywistej Re, ale również względem początku osi urojonej Im, w sposób znany nam doskonale z układu kartezjańskiego .
Postarajmy się więc odnaleźć odległość danej liczby od początku układu współrzędnych. Szybko zauważymy, że możemy skorzystać z własności trójkąta prostokątnego z przyprostokątnymi o wartościach: a równej części rzeczywistej i b równej części urojonej . Wartość bezwzględna będzie określała odległość od początku układu współrzędnych. Aby wyznaczyć wzór na tę odległość - skorzystać musimy z Twierdzenia Pitagorasa, dla trójkąta prostokątnego o przeciwprostokątnej c: . Skoro wartość c równa jest odległości liczby od punktu - oznacza to, że znaleźliśmy ogólny przepis na wartość bezwzględną :
płaszczyzny liczb zespolonych )
Modułem liczby zespolonej (wartością bezwzględną liczby zespolonej ) nazywamy jej odległość od początku układu współrzędnych, określoną wzorem:
|
Stąd też można napisać, że:
kwadratów jej części rzeczywistej i urojonej)
Własności modułu[edytuj]
Moduł liczby zespolonej posiada identyczne własności, co wartość bezwzględna dwumianów:
- Moduł liczby zespolonej , sprzężonej , i przeciwnej :
- Kwadrat modułu liczby zespolonej:
- ,
- Moduł iloczynu liczb zespolonych:
- ,
- Moduł ilorazu liczb zespolonych:
- , o ile ,
Moduł sumy liczb zespolonych ma również szczególne właściwości:
- Moduł sumy liczb zespolonych:
- ,
- Moduł różnicy liczb zespolonych:
- ,
- Moduł części rzeczywistej:
- ,
- Moduł części urojonej:
- ,
Argument liczby zespolonej[edytuj]
Znając już definicję modułu liczby zespolonej - jej odległości od początku układu współrzędnych, możemy liczby zespolone opisać nie tylko za pomocą punktów - ale również za pomocą, wspomnianego we wcześniejszych rozdziałach, wektora o początku w punkcie (0,0) i końcu w punkcie o współrzędnych liczby zespolonej. A długość tego wektora będzie równa modułowi liczby zespolonej.
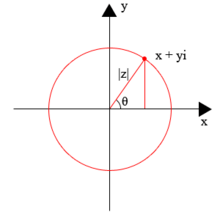

Argrand zauważył, że znając moduł liczby zespolonej - można by spróbować tym parametrem opisać jej wartość. Jednak dla pewnych punktów odległość od początku układu współrzędnych płaszczyzny zespolonej będzie taka sama. O ile dla liczb rzeczywistych moduł określał wartości tylko dwóch liczb (dodatniej i jej przeciwnej), to w przypadku płaszczyzny zespolonej wodząc wektorem o znanej długości zakreślimy okrąg o promieniu - punktów będzie nieskończenie wiele. Potrzebny więc będzie jeszcze jeden argument - jakaś dodatkowa współrzędna. Najlepiej, ogólnie akceptowalna, znana i łatwo otrzymywana w sposób przypominający dotychczas znane działania.
Argrand rozrysowując wektor wpadł na pomysł, w jaki sposób, znając już moduł liczby , tylko jednym dodatkowym argumentem precyzyjnie określić położenie na płaszczyźnie zespolonej. W tym przypadku, wykorzystał ponownie własności trójkąta prostokątnego oraz twierdzenie cosinusów i twierdzenie sinusów, znanych z kartezjańskiego układu współrzędnych. Dzięki nim można było wyznaczyć kąt pomiędzy wektorem opisującym liczbę oraz osią rzeczywistą Re. Kąt ten należy do zbioru liczb rzeczywistych: i nazywany jest argumentem liczby zespolonej.
Z obu twierdzeń, cosinusów i sinusów, Argrand wyprowadził zależności, pozwalające określić argument liczby zespolonej:
Oczywiście, wartość kąta może być znaczna - wodząc wektorem po okręgu, możemy wykonać wiele okrążeń. Dlatego ustalono, że argument główny liczby zespolonej powinien mieścić się w przedziale wartości od 0° do 360° - aby nie zmuszać ludzi do zbędnego wykonywania przeliczeń i wodzenia po okręgu. Obecnie, w dobie skomputeryzowania, miara kątowa uznana jest za archaiczną i wartości kątów podawane są w radianach. Stąd argumentem głównym liczby zespolonej nazywamy kąt ograniczony: .
Liczbę zespoloną w płaszczyźnie zespolonej przedstawić można było do tej pory jako punkt - współrzędne miejsc zerowych - podając na podstawie miejsc zerowych jego współrzędne na osi liczb rzeczywistych Re oraz na osi liczb urojonych Im. Dzięki zabiegom Argranda, od teraz liczby zespolone można przedstawiać również podając ich współrzędne biegunowe .
Przejście z jednego układu współrzędnych do drugiego w matematyce nazwane jest transformacją. W celu transformacji pomiędzy oboma poznanymi układami używamy własności funkcji trygonometrycznych.
| Układ współrzędnych w którym podajemy współrzędne modułu liczby zespolonej i jej argumentu: nazywamy układem współrzędnych biegunowych, a współrzędne - współrzędnymi biegunowymi. |
Argument liczby zespolonej wyznaczyć można wprost z definicji tangensa:
Stąd możemy wyznaczyć wartość kąta , stosując w ogólnym przypadku definicję funkcji odwrotnej do tangensa - arcus tangens:
- Jeśli
- to
Stąd otrzymamy wzór na wartość kąta:
Postać trygonometryczna[edytuj]
Leonhard Euler bardzo zainteresował się pracami Wessela, Gaussa i Arganda. Pozwoliły one bowiem na proste przyswojenie sobie poglądu na liczby zespolone - i potraktowanie ich jako liczb faktycznie istniejących w matematyce.
Dysponując znajomością biegunowego sposobu zapisu liczb zespolonych, na pewno rzucą nam się w oczy pewne zależności, pozwalające zapisać poszczególne części liczby zespolonej jako złożenie funkcji trygonometrycznych. Wystarczy tylko ponownie przyjrzeć się wzorom Argranda z poprzedniego działu. W końcu sam argument liczby zespolonej opisany jest funkcją tangensa.

Zwróćmy więc uwagę, na zależności trygonometryczne trójkąta prostokątnego - skoro w ogólnym przypadku funkcja tangens jest złożeniem funkcji sinus i cosinus, postaci: to warto zbadać wartości tych funkcji dla liczb zespolonych. Zobaczmy więc, z definicji funkcji trygonometrycznych trójkąta prostokątnego, co otrzymamy:
- cosinus kąta ostrego to stosunek długości przyprostokątnej przyległej do kąta, do przeciwprostokątnej
- sinus kąta ostrego to stosunek długości przyprostokątnej przeciwległej do kąta, do przeciwprostokątnej
Dociekliwi zauważą, że w tych równaniach możemy znaleźć trygonometryczny opis dla wartości realnej jak i wyimaginowanej z pomocą parametrów biegunowych.
Stąd też wartość rzeczywistą liczby zespolonej opisać możemy za pomocą jej modułu i cosinusa:
Natomiast wartość urojoną liczby zespolonej opisać możemy za pomocą jej modułu i sinusa:
Podstawiając te wartości do wzoru na postać algebraiczną liczby zespolonej, określoną wzorem:
otrzymamy:
| Każdą liczbę zespoloną można przedstawić w postaci trygonometrycznej:
|
Własności postaci trygonometrycznej[edytuj]
- Jeśli moduł liczby zespolonej , to sama liczba zespolona wynosi zero: oraz jej argument: .
- Dwie liczby zespolone są równe, jeśli ich moduły są równe: oraz argument jednej jest wielokrotnością drugiej, postaci: .
- Mnożenie liczb zespolonych oraz ma postać:
- Słownie przy mnożeniu liczb zespolonych ich moduły mnożymy, a argumenty dodajemy
- Dzielenie liczb zespolonych oraz ma postać:
- Słownie przy dzieleniu liczb zespolonych ich moduły dzielimy, a argumenty odejmujemy
.
Postać wykładnicza[edytuj]
Euler zauważył, że mnożenie i dzielenie liczb zespolonych w postaci trygonometrycznej jest dość charakterystyczne. Jeden czynnik poddawany jest normalnej operacji, a drugi zachowuje się podobnie do wykładnika potęgi. Przypomnijmy sobie, że mnożąc dwie liczby, podnoszone do potęgi y, posiadające tę samą podstawę n, opatrzoną różnymi parametrami x: otrzymamy wynik . Podobieństwo jest zauważalne - przy tej operacji przecież mnożymy dwa parametry x i dodajemy parametry y.
Przeprowadzając skomplikowane dowody matematyczne, na złożonych obliczeniowo szeregach i własnościach logarytmów, udało mu się uzyskać potężne narzędzie łączące ze sobą prawa arytmetyki i algebry - zespolony eksponencjalny (wykładniczy) opis rzeczywistych funkcji trygonometrycznych. Oczywiście, pominiemy wszystkie te niezwykle trudne do ogarnięcia obliczenia i intrygująco brzmiące nazwy, którymi parają się zawodowi matematycy, i przejdziemy do sedna sprawy.
Euler dowiódł, że wartości funkcji trygonometrycznych można zapisać w szczególnej postaci zespolonych potęg liczby o podstawie e (której symbol e nadano właśnie na cześć Eulera):
Stąd wystarczy tylko przeanalizować znany nam wcześniej fragment postaci trygonometrycznej:
Każdą liczbę zespoloną można przedstawić w postaci wykładniczej:
|
Liczby zespolone/Podstawowe zależności
Liczby zespolone/Działania na liczbach zespolonych
Dodawanie liczb zespolonych[edytuj]
Wykonując jakiekolwiek działania na liczbach zespolonych należy pamiętać, że mamy do czynienia z określeniem pozycji punktu w przestrzeni [np. z=(a,b)], czyli tak zwanym wielomianem [a konkretnie dwumianem - w tym przypadku mamy miano określające część rzeczywistą Re(z)=a oraz miano określające część urojoną Im(z)=b]. Działania na liczbach zespolonych wykonywane są więc tak samo jak działania na wielomianach i rządzą się tymi samymi prawami.
| Część rzeczywista sumy dwóch liczb zespolonych jest sumą ich części rzeczywistych, a część urojona tej sumy jest sumą ich części urojonych. |
Suma postaci geometrycznej[edytuj]
Dla dwóch liczb zespolonych:
ich suma wynosi
Suma postaci algebraicznej[edytuj]
Powyższe wynika z łączności dodawania, bowiem algebraicznie:
stąd:
Warto tutaj zauważyć, że dodawanie liczb zespolonych jest przemienne toteż .
Suma liczby zespolonej z jej sprzężeniem[edytuj]
Mając liczbę zespoloną i jej sprzężenie suma liczby zespolonej z jej sprzężeniem wyniesie:
Różnica liczb zespolonych[edytuj]
Analogicznie do sumy, różnica dwóch liczb zespolonych i wynosi , czyli . Słownie oznacza to, że część rzeczywista różnicy dwóch liczb zespolonych jest różnicą ich części rzeczywistych, a część urojona tej różnicy jest różnicą ich części urojonych.
Dowód[edytuj]
Przykłady[edytuj]
Liczby zespolone/Potęgowanie i pierwiastkowanie
Liczby zespolone/Przekształcanie postaci
Liczby zespolone w językach programowania[edytuj]
Teksty[edytuj]
Polskojęzyczne[edytuj]
- Matematyka. Kompendium, Beretelsmann Media, Horyzont 2002;
- Wacław Sierpiński: Zasady algebry wyższej, Warszawa-Wrocław 1946;
- Witold Janowski, Jerzy Kaczmarski: Liczby i zmienne zespolone, WSiP, Warszawa 1974
- T. Jurlewicz, Z. Skoczylas: Algebra liniowa 1. Definicje, twierdzenia, wzory, Oficyna wydawnicza GiS 2004;
- Maciej Grzesiak: Określenie liczb zespolonych, Politechnika Poznańska;
- Zofia Machnicka: Liczby zespolone, WSIZ Rzeszów;
- http://pl.wikipedia.org,
- http://www.math.edu.pl/;
- Matematyka - Liczby zespolone;
Obcojęzyczne[edytuj]
- K. Delventhal, A. Kissner, M. Kulick Grosses Buch der Mathematik, Compact Verlag GmbH 2001;
- T. Andreescu, D. Andrica: Complex Numbers from A to... Z, Birkhäuser 2005;
- J. Reade: Calculus with Complex Numbers, CRC Press 2003;
- Orlando Merino: A Short History of Complex Numbers, University of Rhode Island 2006;
- Resonances, Waves, and Fields, P. Ceperley George Mason University of Fairfax;
- Complex Analysis Project John H. Mathews California State Univ. Fullerton;
- Complex Numbers, Laurie Geller, Math. Dept., University of North Dakota, Grand Forks, ND;
- A Brief History of Complex Numbers, Nicholas Counsell, Math. Dept., University of Bath;
- http://en.wikipedia.org, http://ru.wikipedia.org;
- http://mathworld.wolfram.com;
- Dave's Short Course on Complex Numbers;
- John and Betty's Journey into Complex Numbers;
Nagrania[edytuj]
- Tomasz Miller, Liczby zespolone, kanał Centrum Kopernika Badań Interdyscyplinarnych na YouTube, 23 lutego 2021 [dostęp 2022-03-20].
- Derek Muller, How Imaginary Numbers Were Invented (ang.), kanał Veritasium na YouTube, 1 listopada 2021 [dostęp 2022-03-20].
Licencja[edytuj]
Version 1.2, November 2002
Copyright (C) 2000,2001,2002 Free Software Foundation, Inc.
51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA
Everyone is permitted to copy and distribute verbatim copies
of this license document, but changing it is not allowed.
0. PREAMBLE[edytuj]
The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
1. APPLICABILITY AND DEFINITIONS[edytuj]
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.
The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.
The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.
A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements", "Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING[edytuj]
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY[edytuj]
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS[edytuj]
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
- A. Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
- B. List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
- C. State on the Title page the name of the publisher of the Modified Version, as the publisher.
- D. Preserve all the copyright notices of the Document.
- E. Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
- F. Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
- G. Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
- H. Include an unaltered copy of this License.
- I. Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
- J. Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
- K. For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
- L. Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
- M. Delete any section Entitled "Endorsements". Such a section may not be included in the Modified Version.
- N. Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
- O. Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.
You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties--for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS[edytuj]
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled "Endorsements."
6. COLLECTIONS OF DOCUMENTS[edytuj]
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS[edytuj]
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION[edytuj]
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION[edytuj]
You may not copy, modify, sublicense, or distribute the Document except as expressly provided for under this License. Any other attempt to copy, modify, sublicense or distribute the Document is void, and will automatically terminate your rights under this License. However, parties who have received copies, or rights, from you under this License will not have their licenses terminated so long as such parties remain in full compliance.
10. FUTURE REVISIONS OF THIS LICENSE[edytuj]
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation.
How to use this License for your documents[edytuj]
To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:
Copyright (c) YEAR YOUR NAME.
Permission is granted to copy, distribute and/or modify this document
under the terms of the GNU Free Documentation License, Version 1.2
or any later version published by the Free Software Foundation;
with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
A copy of the license is included in the section entitled "GNU
Free Documentation License".
If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the "with...Texts." line with this:
with the Invariant Sections being LIST THEIR TITLES, with the
Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.
If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.
If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.







































































































































![{\displaystyle z=|z|\cdot \left[\cos(\varphi )+i\sin(\varphi )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e2fa0a8af1b2f188f5e53e7749dc9a2869c0045)







![{\displaystyle z_{1}\cdot z_{2}=|z_{1}\cdot z_{2}|\cdot \left[\cos(\varphi _{1}+\varphi _{2})+i\sin(\varphi _{1}+\varphi _{2})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e362546b8f624ed496e3b495f97959eeae223d7)
![{\displaystyle {\frac {z_{1}}{z_{2}}}=\left|{\frac {z_{1}}{z_{2}}}\right|\cdot \left[\cos(\varphi _{1}-\varphi _{2})+i\sin(\varphi _{1}-\varphi _{2})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb83d21e2f1c64a8283d4728803775dd4eea7c91)
























