Matematyka dla liceum/Funkcje i ich własności/Monotoniczność funkcji

Monotoniczność funkcji oznacza, że funkcja jest:

• rosnąca
• malejąca
• nierosnąca
• niemalejąca
• stała.

Monotoniczność funkcji

monotoniczność funkcji, funkcja rosnąca, funkcja niemalejąca

DEFINICJA Funkcja $f\colon X\to Y$ jest rosnąca w zbiorze $A\subset X$ wtedy i tylko wtedy, gdy dla dowolnych argumentów $x_{1}$ i $x_{2}$ należących do zbioru A i $x_{1}<x_{2}$ wynika $f(x_{1})<f(x_{2})$. $x_{1}<x_{2}\implies f(x_{1})<f(x_{2})$

Inaczej mówiąc wraz ze wzrostem argumentów rosną wartości funkcji.

Analogicznie definiujemy funkcję niemalejącą w zbiorze $A\subset X$, tylko nierówność nie jest ostra. Zachodzi wtedy:

$f(x_{1})\leq f(x_{2})$, dla $x_{1}<x_{2}$

Zauważmy, że gdy nierówność jest rosnąca, to jest również niemalejąca, ale nie musi być odwrotnie.

funkcja malejąca, funkcja nierosnąca

DEFINICJA Funkcja $f\colon X\to Y$ jest malejąca w zbiorze $A\subset X$ wtedy i tylko wtedy, gdy dla dowolnych argumentów $x_{1}$ i $x_{2}$ należących do zbioru A i $x_{1}<x_{2}$ wynika $f(x_{1})>f(x_{2})$. $x_{1}<x_{2}\implies f(x_{1})>f(x_{2})$

Czyli wraz ze wzrostem argumentów maleją wartości funkcji.

Podobnie możemy określić funkcję nierosnącą w zbiorze $A\subset X$. Mamy wtedy:

$f(x_{1})\geq f(x_{2})$, dla $x_{1}<x_{2}$

Gdy nierówność jest malejąca, to jest również nierosnąca, ale nie musi zajść odwrotnie.

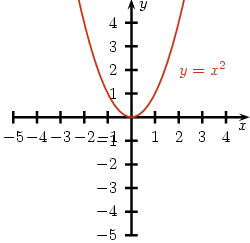
Przykład 1. Przyjrzyjmy się funkcji $y=x^{2}$.

Możemy powiedzieć o tej funkcji, że:

• jest rosnąca dla $x>0$
• jest malejąca dla $x<0$

Przykład 2.

Określmy monotoniczność funkcji na podstawie jej poniższego wykresu. Funkcja ta jest określona dla $x\in [-4;4]$ (czyli $D_{f}=[-4;4]$).

Z wykresu widzimy, że funkcja ta:

• rośnie w przedziałach $(-4;-2)$ oraz $(-1;2)$
• maleje w przedziałach $(-2;-1)$ oraz $(2;4)$

Przykład 3.

Spójrzmy teraz na najprostszy przykład. Jest to funkcja liniowa $f(x)={\frac {4-x}{2}}$. Wykres tej funkcji będzie wyglądał tak:

Widać od razu, że funkcja ta jest malejąca dla wszystkich $x\in \mathbb {R}$.

Przykład 4.

Poniższy wykres przedstawia funkcję niemalejącą.

Nazwa bierze się stąd, że wraz ze wzrostem argumentów nie maleją wartości funkcji, czyli dla coraz wyższych x $f(x)\geq f(x_{0})$, gdzie $x_{0}$ jest dowolną liczbą mniejszą od x.

Przykład 5.

Poniżej przedstawiono wykres funkcji nierosnącej.

Widzimy z wykresu, że wraz ze wzrostem argumentów nie rosną wartości funkcji.

Przykład 6.

Udowodnij na podstawie definicji, że funkcja $f(x)=2x+3$ jest rosnąca.

Funkcję liniową miałeś okazję poznać już w gimnazjum. Wiesz więc od razu, że jeśli współczynnik kierunkowy jest większy od zera to funkcja jest rosnąca. Jednak w zadaniu mam skorzystać z definicji funkcji rosnącej. Czytamy, że funkcja jest rosnąca, gdy dla dowolnego $x_{1}<x_{2}$ zachodzi $f(x_{1})<f(x_{2})$.

Weźmy więc dowolne $x_{1}<x_{2}$ i rozwiązmy nierówność $f(x_{1})<f(x_{2})$.

$f(x_{1})=2\cdot x_{1}+3=2x_{1}+3$

$f(x_{2})=2\cdot x_{2}+3=2x_{2}+3$

$2x_{1}+3<2x_{2}+3$

$2x_{1}+3-2x_{2}-3<0$

$2x_{1}-2x_{2}<0$

$2\cdot (x_{1}-x_{2})<0$

Z założenia mamy, że $x_{1}<x_{2}\implies x_{1}-x_{2}<0$, czyli wartość w nawiasie jest zawsze ujemna. Iloczyn liczby dodatniej (2) i dowolnej liczby ujemnej jest ujemny. Czyli nierówność $f(x_{1})<f(x_{2})$ spełniona jest zawsze, co należało dowieść.