Matematyka dla liceum/Liczby i ich zbiory/Wartość bezwzględna liczby

wartość bezwzględna, definicja wartości bezwzględnej

Definicja

DEFINICJA Wartość bezwzględna liczby jest określona wzorem: $|x|=\left\{{\begin{matrix}x,&{\mbox{ dla }}x\geqslant 0\\-x,&{\mbox{ dla }}x<0\end{matrix}}\right.$.

Wartość bezwzględna liczby nazywana jest także czasami modułem lub wartością absolutną liczby.

Zobaczmy kilka przykładów:

• $|4|=4$
• $|-5|=5$
• $|30-40|=|-10|=10$
• $|4-3|=|1|=1$
• $|3-\pi |=\pi -3$

Bezwzględna wartość to odległość liczby od zera.

Własności

własności wartości bezwzględnej

Dla dowolnych liczb rzeczywistych x i y zachodzą poniższe własności:

• $|x|\geqslant 0$
• $|x|=|-x|$
• $|x|={\sqrt {x^{2}}}$
• $|x\cdot y|=|x|\cdot |y|$
• $\left|{\frac {x}{y}}\right|={\frac {|x|}{|y|}},~y\neq 0$

Interpretacja geometryczna

interpretacja geometryczna wartości bezwzględnej

Wartość bezwzględną liczby można interpretować jako odległość współrzędnej tego punktu od punktu zerowego:

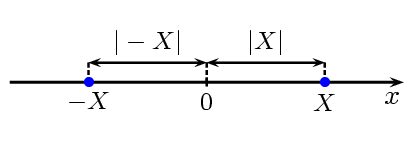
Rozwiązywanie równań z wartością bezwzględną

rozwiązywanie równań z wartością bezwzględną, równania z wartością bezwzględną

Przy rozwiązywaniu równania można wykorzystać własność:

• $|x|=a\iff (x=a\lor x=-a)$

Przykład 1. W przypadku równań z jedną wartością bezwzględną można posłużyć się tylko definicją, np.:

$|x+4|=2$

$x+4=2\lor x+4=-2$

$x=-2\lor x=-6$

Przykład 2. Jeżeli wartości bezwzględnych jest więcej, równanie liczy się inną metodą. Oto przykładowe równanie:

$|x+4|+|x-2|=6$

Tutaj również należy posłużyć się definicją. Pierwsze wyrażenie objęte wartością bezwzględną jest ujemne w przedziale $(-\infty ;-4)$ i dodatnie w przedziale $(-4;+\infty )$. Natomiast drugie wyrażenie jest ujemne w przedziale $(-\infty ;2)$ i dodatnie w przedziale $(2;+\infty )$. Dostajemy więc trzy przedziały, które należy rozpatrzeć (jeśli tego nie widzimy od razu, warto rozrysować sobie cztery wcześniejsze zbiory na osi liczbowej i zobaczyć, jaką pozycję względem siebie zajmują):

1. $(-\infty ;-4)$ gdzie oba wyrażenia są ujemne
2. $[-4;2)$ gdzie pierwsze jest nieujemne a drugie ujemne
3. $[2;+\infty )$ gdzie oba wyrażenia są nieujemne

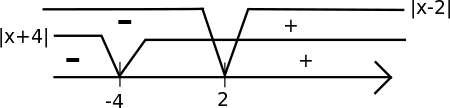
W przypadku pierwszej wartości bezwzględnej, jeżeli $x<(-4)$ trzeba będzie zmienić w niej znaki występujące przy liczbach, gdyż musi ona być dodatnia. Tą metodą tworzy się przedziały. I teraz należy obliczyć równanie do każdego z przedziałów.

$x\in (-\infty ;-4)$

W tym przypadku zmienią się znaki dla każdej wartości bezwzględnej:

$-x-4-x+2=6$

$x=-4$

Liczba ta nie należy do przedziału, więc w przedziale $x\in (-\infty ;-4)$ równanie nie ma rozwiązań.

$x\in [-4;2)$

$x+4-x+2=6$

$6=6$

Tożsamość. Oznacza to, że w przedziale $x\in [-4;2)$ każda liczba spełnia równanie.

$x\in [2;\infty )$

$x+4+x-2=6$

$x=2$

Liczba należy do przedziału, czyli x=2 jest rozwiązaniem równania.

Podsumowując wcześniejsze obliczenia otrzymujemy wniosek, iż:

$x\in [-4;2]$

Przykład 3.

$|x+4|-|2x+3|+3|x-1|=7$

Najprostszą metodą wyznaczania przedziałów jest wyobrażenie sobie liczb pod modułem jako miejsc zerowych funkcji liniowych.

$x+4=0\implies x=-4$

$2x+3=0\implies x=-{3 \over 2}$

$x-1=0\implies x=1$

W ten sposób wyznaczone zostały przedziały, więc teraz wystarczy już tylko wykonać obliczenia.

$x\in (-\infty ;-4)$

$-x-4+2x+3-3x+3=7$

$x=-{5 \over 2}$

W tym przedziale nie ma rozwiązań.

$x\in \left[-4;-{3 \over 2}\right)$

$x+4+2x+3-3x+3=7$

$10=7$

Sprzeczność. W tym przedziale także nie ma rozwiązań.

$x\in \left[-{3 \over 2};1\right)$

$x+4-2x-3-3x+3=7$

$x=-{3 \over 4}$

Ta liczba należy do przedziału, więc jest rozwiązaniem równania.

$x\in [1;\infty )$

$x+4-2x-3+3x-3=7$

$x={9 \over 2}$

Ta liczba należy do przedziału więc jest rozwiązaniem równania.

Podsumowując:

$x\in \left\{-{3 \over 4};{9 \over 2}\right\}$

To samo można zapisać w postaci:

$x=-{3 \over 4}\lor x={9 \over 2}$

Rozwiązywanie nierówności z wartością bezwzględną

rozwiązywanie nierówności z wartością bezwzględną, nierówności z wartością bezwzględną

Przy rozwiązywaniu nierówności można wykorzystać poniższe własności:

• $|x|<a\iff -a<x<a\iff (x>-a\land x<a)$
• $|x|\leqslant a\iff -a\leqslant x\leqslant a\iff (x\geqslant -a\land x\leqslant a)$
• $|x|>a\iff (x<-a\lor x>a)$
• $|x|\geqslant a\iff (x\leqslant -a\lor x\geqslant a)$

W przypadku niektórych nierówności możemy posłużyć się którąś z powyższych własności np.:

$|x+5|\leqslant 10$ wykorzystując własność $|x|\leqslant a\iff (x\geqslant -a\land x\leqslant a)$, gdzie zamiast x postawiamy x+5, a zamiast a liczbę 10 otrzymujemy:

$|x+5|\leqslant 10\iff (x+5\geqslant -10\land x+5\leqslant 10)$

$(x\geqslant -15\land x\leqslant 5)$

Odp. $x\in [-15;5]$.