Tworzenie rysunków

Rysunki 2D

plot

Rysunki dwuwymiarowe można tworzyć za pomocą funkcji plot. Najczęstsze użycie to:

plot(x, y)

Oba argumenty są wektorami tej samej długości i zawierają współrzędnych odpowiednio x-owe i y-owe.

Zatem plot dostaje ciąg punktów: $P_{i}=(x_{i},y_{i})$ i rysuje linie: $P_{1}-P_{2},...,P_{n-1}-P_{n}$ . Na przykład:

x=[0:1:10]
y=sin(x)
plot(x,y)

Dostajemy przybliżenie wykresu funkcji sinus.

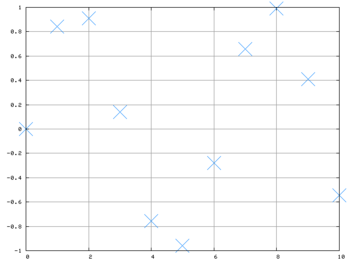
Punkty domyślnie zostały połączone liniami i narysowane na czerwono. To można zmienić, np.

plot(x,y,"+b")

zaznaczy punkty znakami $\times$ i narysuje je na niebiesko. Żeby lepiej było widać chcemy też wyświetlić kratę punktów:

grid on

Dostępne kolory i ich oznaczenia:

oznaczenie literowe	oznaczenie numeryczne	nazwa koloru
k	0	black
r	1	red (domyślny)
g	2	green
b	3	blue
m	4	magenta
c	5	cyan
w	6	brown

Dostepne style to:

+ * o x - . @ -@

Wykresy można łączyć. Każdy z nich wówczas dobrze jest narysować innym kolorem i opisać w legendzie. Opis umieszcza się między dwoma średnikami, na przykład:

 t = [0:0.1:10];
 plot(
   t,cos(t),"-r;cos(t);",
   t,sin(t),"+m;sin(t);",
   t,tan(t),"xc;tan(t);",
   t,atan(t),"*g;argtan(t);" );

W tym wykresie funkcja tangens eksploduje, więc przyda się jeszcze ograniczyć zakres osi:

 axis( [0 10 -2 2] )

pcolor

vZx = linspace(-5,5,200);
vZy = linspace(-5,5,200);
[Zx,Zy]=meshgrid(vZx,vZy);
a = sqrt(Zx.^2 + Zy.^2);
# ---------- draw ----------------
clf #  clear the screen
pcolor(Zx,Zy,a)
colormap(jet(32));
title('Absolute value of zx+zy*i')
xlabel('zx')
ylabel('zy')
shading interp 
colorbar

lub z użyciem funkcji trygonometrycznych

# http://yapso.sourceforge.net/demo/demo.html
[x,y] = meshgrid(linspace(-pi,pi,30));
z = cos(x).*sin(y);

subplot(1,2,1)
title('Demo of pcolor: shading flat');
pcolor(x,y,z);
shading flat

subplot(1,2,2)
title('shading interp');
pcolor(x,y,z);
shading interp

Rysunki 3D

Narysować domek za pomocą funkcji mesh.

mesh(x,y,z)

rysuje wykres dla punktów $(x_{i},y_{j},z_{i,j})$ . Zatem domek o kwadratowej podstawie $[0,1]^{2}$ , wysokości $1$ i o dachu wysokości $1$ można narysować za pomocą komendy:

mesh([0 0.5 1], [0  1], [1 2 1; 1 2 1 ])

Narysować za pomocą za pomocą funkcji mesh i meshgrid wykres funkcji

f:[-1,1]^{2}\to \mathbb {R}

f(x,y)=sin(x^{2}+2y^{2})\,

Przygotujmy brzegi:

x=[-1:0.1:1];
y=[-1:0.1:1];

Obliczamy wartości:

[X,Y]=meshgrid(x,y);
Z=sin(X.*X.+2.*Y.*Y)

Rysujemy:

mesh(x,y,Z)

Zapis do pliku

Sposób zapisu do pliku zależy od wersji GNU Octave.

Jeśli rysujemy za pomocą Gnuplota, można to zrobić "niskopoziomowo" za pomocą __gnuplot_raw__:

__gnuplot_raw__("set term png \n");
__gnuplot_raw__("set output \"plik.png\" \n");
plot(...)

Wynikiem będzie "plik.png" w formacie PNG.

Inna metoda, już odradzana, to użycie funkcji gset

gset term postscript eps color
gset output "plik.eps"
plot(...)

Zaawansowany gnuplot

Z poziomu Octave'a można użyć zaawansowanych opcji Gnuplota. Wykonując

__gnuplot_raw__("polecenie\n");

to tak, jakbyśmy wykonywali polecenie w samym gnuplocie. Na przykład:

__gnuplot_raw__("set key off\n")

Przetwarzanie obrazów

Obraz jest reprezentowany przez macierz 2D zawierającą kolory. Dzięki temu bardzo łatwe jest przetwarzanie i analizowanie obrazów w Octave^[1]^[2]^[3]

pkg load image;
pkg load miscellaneous; # waitbar
nx = 480;
ny = 480;
MyImage = zeros(ny,nx,3); # 2D matrix filled with zeros
 waitbar(0,'Please wait...'); # info
for iy = 1:ny
  for ix= 1:nx
  # tu możemy zmieniać kolor poszczególnych pikseli
  
  end # for ix
 waitbar(iy/ny);
end # for iy
image(MyImage); # wyświetla obraz
imwrite(MyImage,'s.png' ); # zapisuje obraz do pliku s.png ; wymaga ImageMagic

Bardziej zaawansowany przykład :

# octave m-file based on the m-file by Chris King
# http://www.dhushara.com/DarkHeart/Viewers/source/siegel.m
# an MyImage here is a matrix for 24 bit (3 byte) colors 

# load packages
pkg load image; # imwrite
pkg load miscellaneous; # waitbar

# constan values 
nx = 480;
ny = 480;
MyImage = zeros(ny,nx,3); # 2D matrix filled with zeros
magc=0.65;
dSide=1/magc;
Zxmin = -dSide;
Zxmax = dSide;
Zymin = -dSide;
Zymax = dSide;

stepy = (Zymax - Zymin)/(ny - 1);
stepx = (Zxmax - Zxmin)/(nx - 1);

# computations 
waitbar(0,'Please wait...'); # info 
for iy = 1:ny
  Zy = Zymax - iy*stepy; # invert y axis
  for ix= 1:nx
    Zx = Zxmin + ix*stepx;
    if(Zy>0 && Zx>0)  # first quadrant should be in upper right position
    MyImage(iy,ix,2)=255-MyImage(iy,ix,2);
    endif;
  end # for ix
  waitbar(iy/ny);
end # for iy
# 
image(MyImage); # display image 
imwrite(MyImage,'s.png' ); # save image to the file

Ogólny schemat przetwarzania obrazów :^[4]

I = imread ("my_input_image.img");
J = process_my_image (I);
imwrite ("my_output_image.img", J);

imwrite z Octave ma odwróconą listę argumentów w stosunku do MATLAB'a "

imwrite(filename, image)  % Octave
imwrite(image, filename)  % MATLAB

Jednak w Octave funkacja wykrywa kolejność argumentów więc nie ma się o co martwić^[5]

Typy obrazów

RGB = macierz M x N x 3 gdzie każdy 3-wektor odpowiada intensywności R-G-B
indeksowany = macierz M x N liczb całkowitych odpowiadających kolejności kolory w macierzy kolorów
skali szarości = macierz M x N liczb odpowiadających intensywności szarości
binarne = macierz M x N wartości logicznych

Indeksowane

Indeksowane obrazy korzystają z mapy kolorów ( palety).

# color map = mapa kolorów ( paleta) jest macierzą trójek RGB = liczb od 0.0 do 1.0
cm = [
0 0 0   % pierwszy element = czarny kolor
0 0 1   % niebieski
0 1 0   % zielony
0.2 0.2 0.2   % szary
1 0 0   % czerwony
1 0 1   % purpurowy
1 1 0   % żółty
1 1 1]; % ostatni element = biel

r=rows(cm); # liczba wierszy i kolorów
c=columns(cm); # liczba kolumn , powinna być 3 

iSide=100; # długość boku obrazu w pixelach

img = 4*ones(iSide,iSide); # używamy 4 kolor z mapy kolorów 

colormap(cm);
image(img)
imwrite(img,"cm.png")

lub :^[6]

## Show the 'hsv' colormap as an image
image (1:64, linspace (0, 1, 64), repmat (1:64, 64, 1)')
axis ([1, 64, 0, 1], "ticy", "xy")
colormap hsv

Aby zobaczyć co zawiera mapa kolorów wpisujemy jej nazwę bez średnika :

jet

Losowe kolory :

# array of random integers from 1 to r 
# add 1 to remove zero 
img = floor(rand(iSide,iSide).*r ).+ 1; # Element-wise operations

Zródła

« Aproksymacja wielomianowa w przestrzeni Hilberta

Spis treści

Źródła »

[1] tave doc - Image-Processing

[2] Introduction to image processing in Matlab 1 by Kristian Sandberg

[3] Matrixlab - rgb examples

[4] tave doc : Image Processing

[5] Peter Kovesi - info about octave/matlab

[6] st Colormap demos? by Soren Hauberg

[1]

[2]

[3]

[4]

[5]

[6]