Matematyka dla liceum/Planimetria/Czworokąty i ich własności

Czworokąt to wielokąt płaski o czterech bokach.

Podział czworokątów:

• wklęsłe
• wypukłe: trapezoidy, deltoidy, trapezy, równoległoboki, romby, prostokąty, kwadraty.

Klasyfikacja czworokątów:

Charakterystyka czworokątów

Deltoid

DEFINICJA Deltoid jest to czworokąt wypukły, który ma oś symetrii zawierającą jedną z jego przekątnych.

P = 1/2 |DB| * |AC|

Trapez

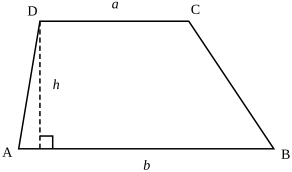
DEFINICJA Trapez jest to czworokąt, który ma przynajmniej jedną parę boków równoległych.

• Wysokością trapezu nazywamy odcinek zawarty między prostymi zawierającymi jego podstawy i prostopadły do nich.

Równoległobok

DEFINICJA Równoległobok jest to czworokąt, który ma dwie pary boków równoległych.

Równoległobokiem nazywamy taki czworokąt, który spełnia chociaż jeden z warunków:

1. Przeciwległe boki są równoległe
2. Przeciwległe boki są tej samej długości
3. Przekątne dzielą się na połowy
4. Przeciwległe kąty są równe
5. Suma miar kątów przylegających do każdego boku jest równa 180^o

• Obwód równoległoboku= 2a + 2b
• Pole równoległoboku = a* h = a * b * sin α

Romb

DEFINICJA Romb jest to równoległobok, którego wszystkie boki są równe.

Własności rombu:

• AB, BC, DC, AD = a – boki rombu
• AC = d1 oraz BD = d2 – przekątne rombu
• d1 , d2 – długości przekątnych rombu
• h – długość wysokości rombu
• r – długość promienia okręgu wpisanego w romb
• kąt alfa – miara kąta ostrego, jaki tworzą boki rombu

W czworokącie tym przekątne dzielą się na połowy i przecinają się pod kątem prostym.

Miejsce przecięcia przekątnych (d1 i d2, które przecinają się pod kątem prostym) jest środkiem okręgu wpisanego.

Promień (r) jest połową jego wysokości (h).

Wzory:

Pole rombu

• P = a*h
• P = (d1*d2) / 2
• P = 2a * r
• P = a2 * sin alfa

Obwód rombu = 4a

Prostokąt

DEFINICJA Prostokąt jest to czworokąt, którego wszystkie kąty są równe (i wynoszą 90°).

Kwadrat

DEFINICJA Kwadrat jest to czworokąt, którego wszystkie kąty i boki są równe.

Punkt przecięcia się przekątnych kwadratu wyznacza:

• środek okręgu opisanego na kwadracie, którego promień R jest równy połowie długości przekątnej kwadratu
• Środek okręgu wpisanego w kwadrat, którego promień r jest równy połowie długości boku (a) kwadratu.

Pole kwadratu:

• P = a²
• P = ½ d²
• P = R²
• P= (2r)²

Długość przekątnej kwadratu: a pierwiastek z 2

Długość promienia okręgu opisanego na kwadracie: R= ½ d = ${\operatorname{a}\sqrt(2)\over\operatorname{2}}$

Długość promienia okręgu wpisanego w kwadrat: r = ½ a

Do zrobienia: Dodanie rysunków i większej ilości własności czworokątów