Fale/Układy fizyczne, a jego drgania swobodne
Licencja
|
|---|
|
Autor: Mirosław Makowiecki
Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność. |
Podręcznik: Fale.
Ruchem drgającym harmonicznym nazywamy drgania, które zależą od częstotliwości kołowej drgań własnych ω i przesunięcia fazowego φ. Drgania te opisujemy względem czasu "t" wzorem:

Ruch pokazany przy pomocy równości (1.1), są to ruchy o jednym stopniu swobody. Okresem drgań harmonicznych nazywamy odwrotność częstości ν, którą możemy przepisać przy pomocy definicji częstotliwości kołowej:

Siła kierujące i bezwładność ciała dla drgań o jednym stopniu swobody[edytuj]
Ruch harmoniczny (1.1) jest rezultatem działania dwóch przeciwstawnych czynników, tzn. siły kierującej i bezwładności. Siła kierująca w ruchu harmonicznym usiłuje przywrócić układ do stanu równowagi, a bezwładność jest cechą układu, która przeciwstawia się zmianom ruchu układu.
Drgania tłumione[edytuj]
Ruch harmoniczny opisywany wzorem (1.1) nie jest ruchem tłumionym, bo jego amplituda nie zmienia się w miarę upływu czasu. W ruchu tłumionym, amplituda drgań maleje z czasem. Przykładem drgań gasnących są drgania opisane równością:

Wahadło matematyczne[edytuj]
Wahadłem matematycznym nazywamy układ, w którym ciało o masie M jest zawieszone na nieważkiej nici lub pręcie o długości l. Siłą kierującą w ruchu wahadła jest składowa siły grawitacji prostopadła do nici, jej wartość określa wzór F=Mg sinψ, to z drugiej zasady dynamiki Newtona w tym przypadku wynika:

Funkcję sinus możemy rozłożyć w szereg Taylora, którego zapis dla naszej funkcji jest następujący:

Dla małych kątów ψ, można pominąć wszystkie wyrazy szeregu poza pierwszym, wówczas równość (1.4) możemy przestawić (1.5):

Rozwiązaniem równania (1.6) są funkcje harmoniczne w postaci (1.1) (co udowodnimy poniżej), dla której druga pochodna tego właśnie przypuszczalnego rozwiązania naszej funkcji jest:

Jeśli funkcję (1.7) wraz (1.1) podstawimy do wzoru (1.6), w ten sposób otrzymamy tożsamość, co dowodzi o harmoniczności ruchu masy M w wahadle matematycznym.
Ciężarek o masie M przyczepiony do dwóch sprężynek[edytuj]
Rozważmy dwie sprężynki przyczepione do ścianek i połączone ze sobą poprzez masę M. Sprężynki mają znikomą masę. Całkowita siła działająca na masę M jest wyrażona:

Ruch ciężarka możemy opisać drugim prawem dynamiki Newtona, który piszemy:

Ruch ciała M będziemy opisywać funkcją ψ(t), którą definiujemy jako starą funkcję z(t) minus stałą "a", zatem w (1.9) możemy dokonać zamiany zmiennych według:

Równanie (1.9) przy pomocy podstawienia (1.10), którym występuje poszukiwana funkcja ψ(t) jest zależna od czasu, dla równania, która jest równaniem oscylatora harmonicznego, możemy zapisać w postaci:

Kwadrat częstości kołowej ruchu harmonicznego ciała, a także rozwiązanie ruchu (1.9) na podstawie (1.11) i (1.10), przestawiamy:


Drgania poprzeczne ciężarka przyczepionego do sprężyn[edytuj]

Rozważmy ciężarek o masie M przyczepiony do dwóch nieważkich sprężyn. Współczynnik sprężystości sprężyn wynosi K. W położeniu równowagi każda ze sprężyn zostaje napięta do długości a. Opisywany układ może wykonywać dwa rodzaje drgań poprzecznych i jedno drganie podłużne. W stanie równowagi siła działająca na ciało z jednej ze sprężyn jest opisywana:

Opisu drgań podłużnych nie będziemy powtarzać, ponieważ jest zamieszczony w poprzednim rozdziale. W drganiach poprzecznych siła, z jaką pojedyncza sprężyna działa na ciężarek M, jest opisana wzorem:

Z drugiej zasady dynamiki Newtona ruch opisujący drgania poprzeczne jest opisywany przez równanie różniczkowe:

Należy zauważyć, że długość l występująca po prawej stronie wzoru końcowego (1.16) jest funkcją w ogólności od zmiennej x.
Mała długość swobodna sprężyny jako pierwsze przybliżenie[edytuj]
Równanie ruchu ciała o masie M (1.16) w przybliżeniu małej długości sprężyny, tzn. stosunek długości sprężyny swobodnej a0 przez długość sprężyny l jest w naszym przypadku tutaj rozważanym wielkością pomijalną. Równanie ruchu (1.16) przybliżeniu tutaj omawianym jest w postaci:

Wzór (1.17) uzyskaliśmy na podstawie dokładnego rozwiązania (1.16), w której definicja kwadratu częstotliwości kołowej dla przybliżenia małej długości sprężyny przy zachodzącym (1.14) jest:

Rozwiązaniem równania ruchu (1.17) jest to równanie zależne od częstotliwości kołowej ω, które jest opisane wzorem (1.1). Widzimy, ze zgodnie ze wzorami (1.18) i (1.12), że częstość drgań poprzecznych w naszym przybliżeniu jest równa częstości drgań podłużnych w ruchu drgającym ciała o masie M.
Przybliżenie małych drgań[edytuj]
Aby rozwiązać równanie różniczkowe (1.16) stosowaliśmy przybliżenia małej długości swobodnej sprężyny, wtedy stosunek długości swobodnej sprężyny a0 do długości aktualnej sprężyny jest względnie mały, których stosunek w takiej sytuacji możemy pominąć. Jeśli tego stosunku nie można pominąć, to możemy powiedzieć, że dla małego ε, względem którego będziemy rozkładali odwrotność długości chwilowej sprężyny w szereg Taylora, który to podstawimy do równania różniczkowego (1.16), i pominiemy wyrazy wyższe niż liniowe, w ten sposób dojdziemy do równania różniczkowego, które jest równaniem różniczkowym ruchu harmonicznego, to co chcieliśmy otrzymać. Zatem napiszmy teraz definicję kwadratu chwilowej długości sprężyny "l" i kwadratu wielkości ε:


Odwrotność długości sprężyny liczymy rozkładając tę odwrotność w szereg Taylora względem zmiennej x, która jest położeniem ciała o masie M:

Wzór (1.21) podstawiamy do (1.16) do odjemnika w nawiasie, w ten sposób możemy otrzymać równość zależną od zmiennej x, którego to równanie jest równaniem oscylatora harmonicznego:
![{\displaystyle {{d^{2}x} \over {dt^{2}}}=-{{2Kx} \over {M}}\left(1-{{a_{0}} \over {l}}\right)=-{{2Kx} \over {M}}\left(1-{{1} \over {2}}\epsilon +{{3} \over {8}}\epsilon ^{2}-...\right)\simeq -{{2Kx} \over {M}}\left[1-{{a_{0}} \over {a}}\left(1-{{1} \over {2}}{{x^{2}} \over {a^{2}}}+...\right)\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f58481fe6ee175ef08eaa2ed3c860d978801db0)
Równanie ruchu (1.22) możemy przepisać dokonując odpowiednich przekształceń w nawiasie w końcowej wspomnianej tożsamości:

W równaniu ruchu masy M zapisaną w punkcie (1.23) możemy pominąć wyższe wyrazy niż liniowe przy przybliżeniu małych drgań, by potem wykorzystać wzór (1.14):

Kwadrat częstotliwości kołowej ruchu drgającego drgań poprzecznych wynika z równania różniczkowego (1.24):

Rozwiązanie równania ruchu (1.24) przy definicji kwadratu częstotliwości kołowej (1.25) jest równaniem zapisane w punkcie (1.1). Możemy wyznaczyć iloraz częstotliwość drgań podłużnych (1.12) przez częstotliwość kołową drgań poprzecznych (1.25) przy oznaczeniu (1.14) w następującej postaci:

Patrząc na wzór (1.26), gdy długość własna sprężyny a0 jest względnie mała w porównaniu z długością sprężyny w stanie równowagi "a", to częstotliwości kołowe drgań podłużnych i poprzecznych są sobie w przybliżeniu równe.
Obwód LC, czyli solenoid z dwoma kondensatorami[edytuj]

Równanie opisujących układ LC z dwoma kondensatorami o pojemności C i z cewką od indukcji elektrycznej L przestawiamy:

Ładunek Q1 jest powiązany z ładunkiem Q2, a także ten drugi ładunek jest powiązany z natężeniem prądu elektrycznego płynącego w obwodzie:


Równanie (1.27) możemy tak napisać przy wykorzystaniu tożsamości (1.28), które to możemy dalej zróżniczkować obustronnie względem czasu przy wykorzystaniu (1.29), wtedy otrzymamy równość różniczkową drugiego stopnia:

Końcowe równanie (1.30) jest równaniem oscylatora harmonicznego, którego kwadrat częstotliwości kołowej przestawiamy:

Natężenie prądu elektrycznego, który jest rozwiązaniem równania różniczkowego (1.30) przestawiamy podobnym wzorem do (1.1), jest to równanie w postaci:

Zasada superpozycji i liniowość równań ruchu[edytuj]
Omawiane tutaj były przypadki, w których siła kierunkowa była wprost proporcjonalna do ψ(t), natomiast niezależała od wyższych potęg ψ, tzn. ψ2,ψ3,.... Równanie niezawierające wyższych potęg ψ niż pierwszego stopnia nazywamy równaniem liniowym. Gdy w naszym równaniu występują wyższe potęgi niż pierwszego stopnia, tak powstałe równanie nazywamy nieliniowym. Natomiast, gdy równanie nie zawiera wyrazów z niezależnych od ψ nazywamy równaniem jednorodnym.
Wprowadzenie do równań liniowych jednorodnych[edytuj]
Równania liniowe i jednorodne różniczkowe mają tę właściwość, że suma dwóch rozwiązań równania liniowego i jednorodnego też spełnia równanie liniowe i jednorodne, co jest wiadomo. Udowodnimy czy też jest dla równań różniczkowych nieliniowych, że jeśli mamy dwa rozwiązania poniższego równania różniczkowego, to suma ich ma spełniać też to równanie, jak wykażemy co jest jedynie możliwe, gdy mamy równanie różniczkowe liniowe. A oto mamy równość różniczkową w ogólności zależną od wyższych potęg niż pierwszego stopnia:

Weźmy dwa rozwiązania ψ1 i ψ2, które spełniają równanie różniczkowe (1.33):


Sumę rozwiązań ψa i ψb też spełnia równanie różniczkowe (1.33) jak i składowe tejże sumy:

Równanie (1.34) możemy dodać do (1.35) do siebie i porównać ze wzorem (1.36), w ten sposób otrzymujemy tożsamości:




Równanie (1.37) i (1.38) są tożsamościami, tzn. które są zawsze spełnione, a równości (1.39) i (1.40) są zawsze spełnione tylko dla α=0 i β=0, zatem co zachodzi tylko dla rozwiązania liniowego przy postawionych warunkach powyżej, to superpozycja rozwiązań równania różniczkowego liniowego jest też rozwiązaniem tego samego równania różniczkowego. Co kończy dowód.
Warunki początkowe a superpozycja rozwiązań[edytuj]
Załóżmy, że mamy dwa rozwiązania jako szczególne rozwiązania w chwilach szczególnych ψ1(0) i ψ2(0), które odpowiadają warunkom brzegowym rozwiązań ψ1(t) i ψ2(t), a rozwiązania równania będące superpozycją naszych rozwiązań, czyli ψ1(t)+ψ2(t), odpowiadają warunki brzegowe w postaci: ψ1(0)+ψ2(0).
Niejednorodne równanie liniowe[edytuj]
Wprowadźmy do równania liniowego siłę wymuszającą F(t) zależną od czasu, wtedy po tej operacji otrzymujemy równanie różniczkowe:

Załóżmy, że mamy dwa równania różniczkowe (1.41), każde odpowiada innej sile wymuszającej, to superpozycja dwóch rozwiązań spełnia równanie różniczkowe odpowiadające sumie dwóch sił wymuszających w równaniu (1.41), tzn. F1(t)+F2(t).
Wahadło sferyczne[edytuj]
W celu zilustrowania zasady superpozycji rozpatrzmy wahadło sferyczne zawieszone na nieważkiej nici, która posiada możliwość ruchu w dowolnym kierunku. Położenie równowagi znajduje się w punkcie x=0 i y=0, co równania ruchu takiego wahadła piszemy:


Powyższe dwa równania są rozdzielone, tzn. każde równanie zależy od innych zmiennych i ich rozwiązania są niezależne i są opisywane wzorami tylko od zmiennej t i są to dwa rozwiązania:


Kwadrat częstotliwości kołowej występujących w rozwiązaniach (1.44) i (1.45) wynikających z równań (1.42) i (1.43) zapisujemy wzorem (1.6).
Układy o dwóch stopniach swobody i jego drgania swobodne[edytuj]
Opis układów w ogólnej konfiguracji wymaga znajomości dwóch zmiennych, tzn. ψa i ψb, co oznacza np. ruch wahadła wokół płaszczyzn wzajemnie prostopadłych kierunkach w płaszczyźnie drgań, a w przypadku układów LC, co oznacza, że ψa i ψb oznaczają ładunki na dwóch kondensatorach lub też natężenia prądów elektrycznych. Najbardziej ogólny ruch harmoniczny jest superpozycja dwóch drgań harmonicznych, których jak wiemy też jest w pewnym senie ruchem harmonicznych. Składowe tych rozważanych drgań harmonicznych nazywamy drganiami normalnymi lub drganiami własnymi. Można tak dobrać warunki początkowe, by układ wykonywał jedno lub drugie drganie harmoniczne. Załóżmy, że układ wykonuje drgania z częstotliwościami kołowymi ω1 i ω2. Przesunięcia fazowe dla obu drgań normalnych są sobie równe. Dla obu tychże drgań wychylenia od stanu równowagi są opisywane przez:


Dla drugiej postaci drgań normalnych, zachodzą podobne związki jak w punktach (1.46) I (1.47), tylko jedynkę zamieniamy na dwójkę. W ogólnej konfiguracji wychylenia od położenia równowagi dla ψa i ψb zapisujemy jako superpozycja drgań harmonicznych o częstotliwościach ω1 i ω2:

a dla drugiej zmiennej, tzn. ψb drgania opisujemy:

Wahadło sferyczne jako układ drgający o dwóch stopniach swobody[edytuj]
Dla wahadła sferycznego na podstawie równań różniczkowy opisujący te nasze drgania , tzn. równań (1.42) i (1.43) dla dwóch niezależnych drgań, tzn. w niezależnych zmiennych, dla którego kwadrat częstotliwości kołowej jest opisywany wzorem (1.6), których to wychylenia od stanu równowagi dla tych rozważanych zmiennych są przestawione jako:


Przybliżenie harmoniczne dla dwuwymiarowego układu współrzędnych[edytuj]
Rysunek obok przestawia ruch ciała o masie M przyczepionych do czterech sprężyn o stałych proporcjonalnych K1 i K2, które są przyczepione do odpowiednich ścianek. Masy sprężynek są w przybliżeniu zerowe w porównaniu z masą kulki M. Kulka może wykonywać dwa niezależne drgania wzdłuż osi iksowej i igrekowej lub w postaci złożenia tychże drgań. We wzorach opisujących ruch masy M pomijamy człony x2/a2, y2/a2 i xy/a2. W ten sposób możemy napisać przybliżenie klasyczne małych drgań. Jeśli dokonamy odpowiedniego małego przesunięcia ciała M w kierunku osi iksowej, to wtedy z dokładnością do wyrazów wyżej podanych otrzymamy wzór na siłę iksową i igrekową w postaci:


Podobnie postępujemy, gdy dokonamy małego przesunięcia wzdłuż osi igrekowej. Ogólne równania ruchu opisujące drgania masy M są to równania ruchu zapisane w przybliżeniu małej długości sprężyny, które możemy napisać je jako dwa równania opisujące ruch ciała M na płaszczyźnie xy, których rozwiązania są superpozycją drgań wzdłuż osi iksowej i igrekowej:


Rozwiązania równania (1.54), a także kwadrat częstotliwości kołowej możemy zapisać w postaci poniższych tożsamości:


Wychylenie od punktu początkowego względem osi igrekowej jako rozwiązanie równania różniczkowego (1.55) i kwadrat jej częstotliwości kołowej piszemy:


Współrzędne normalne w układzie obróconym o pewien kąt[edytuj]
Albowiem równania (1.54) i (1.55) opisują ruchy harmoniczne, ale w ogólności to ma ogólnych rozwiązań w postaci rozwiązań (1.48) i (1.49). W naszym przypadku opisujące ruch harmoniczny. Aby łatwiej można było opisywać ruch harmoniczny kulki wprowadza się współrzędne x'. y', które są obliczone względem starych współrzędnych obrócone o kąt α, których są kombinacjami liniowymi współrzędnych starych x i y. Są to współrzędne, których równania ruchu masy M opisywane są względem jednej współrzędnej, a każde równanie różniczkowe zależy od innej zmiennej. W ogólnym przypadku wybór współrzędnych normalnych nie jest taki łatwy. Zazwyczaj jest tak, że równania ruchu zawierają współrzędne x i y wziętej razem. W ogólnym przypadku prosta transformacja nie wystarcza i należy dokonać ogólnej transformacji liniowej w układzie równań różniczkowych opisujących nasze ruchy, by w ten sposób każde równanie było opisywane we współrzędnych normalnych, tzn. każde równanie zależało tylko od jednej zmiennej.
Rozwiązywanie równań różniczkowych ruchu[edytuj]
Załóżmy, że mamy układ fizyczny, która drga, który jest opisywany przy pomocy równań różniczkowych zapisane we współrzędnych x i y w postaci:


Przyjmijmy, że rozwiązaniami równań ruchu (1.60) i (1.61) są to rozwiązania w postaci funkcji x i y, które są opisywane w postaci funkcji zależnych od czasu i są zależne od takiego samego przesunięcia fazowego.


Jeśli układ wykonuje drgania normalne wzdłuż jednej osi, to wtedy równania (1.60) i (1.61) są opisywane równaniami dla każdego ruchu z osobna:


W ogólnym przypadku, gdy nie mamy doczynienia ze współrzędnymi normalnymi, to wtedy należy rozwiązania (1.62) i (1.63) podstawić do (1.60) i (1.65), w ten sposób otrzymać następujący układ równań:


Z równań (1.63) i (1.67) możemy wyznaczyć stosunek x/y wedle następujących sposobów:


Warunkiem koniecznym by rozwiązać równania różniczkowe ruchu (1.60) i (1.61), jest równość obu stron (1.68) i (1.69), co prowadzi do:

Równanie (1.70) jest równaniem kwadratowym względem zmiennych ω2, którego rozwiązaniem są dwa kwadraty częstotliwości ω12 i ω22. Stosunek y/z względem równości (1.68) dla jednej i drugiej postaci drgań normalnych nazywamy stosunkiem w postaci:


Rozwiązaniami równania różniczkowego falowego (1.60) i (1.61) dla współrzędnej x jest superpozycją rozwiązań równania falowego dla częstotliwości ω1 i ω2, co jest to rozwiązaniem w postaci:

A rozwiązaniami y(y) według (1.72) są to rozwiązania przestawione w postaci równania:

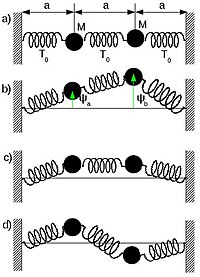
Drgania podłużne, układ sprężynek i ciężarków[edytuj]
Rozpatrzmy układ trzech sprężynek o masie zaniedbywanej, w których dwie sprężynki są połączone ze ściankami, a sprężynka środkowa jest połączona z ciężarkami o masie M. Rozważmy sytuację, gdy dwa ciężarki są przesunięte o to samo przesunięcie, wtedy sprężynka środkowa nie jest napięta, Siła z jaką sprężynka działa na pierwsze ciało jest określona wzorem F1=-Kψa, a na drugie ciało wzorem F2=-Kψb, przy założeniu ψa=ψb, i pamiętając że sprężynka środkowa nie oddziaływuje w takim przypadku z ciężarkami, równanie ruchu jest opisane:


Kwadrat częstotliwości kołowej z jaką drga ten układ dwóch mas jest określony przez wzór:

Rozważmy teraz sytuację, gdy ψa=-ψb, wtedy siła działająca na pierwszy ciężarek, której wartość jest równa potrojonej wartości współczynnika sprężystości i przesunięcia od stanu równowagi ciężarka pierwszego, której kierunek tej siły jest przeciwny niż kierunek osi zet:

A całkowita siła działająca na drugi ciężarek, której wartość jest równa potrojonej wartości współczynnika sprężystości i przesunięcia od stanu równowagi ciężarka pierwszego, kierunek tej siły jest przeciwny niż kierunek osi zet:

Równania ruchu dla ciężarka pierwszego i drugiego są określone przez wzory wynikających z drugiego prawa Newtona:


Kwadrat częstotliwości drgań swobodnych drgań normalnych, który dla drgań dwóch ciężarków opisywanych przez równania różniczkowe (1.80) i (1.81), przestawiamy:

Na podstawie przypadków szczególnych jakie dokonaliśmy w powyższych rozważaniach dowiadujemy się, że układ może drgać na dwa sposoby, której kwadrat częstotliwości jest opisany wzorem (1.77) lub (1.82).
Rozważmy teraz przypadek ogólny, w którym opisywać będziemy ruch dwóch tych ciężarków, które są opisywane równaniami wynikających z drugiego prawa Newtona:


Równania (1.83) i (1.84) możemy do siebie dodać i je odjąć, w ten sposób otrzymać następne dwa równania zależne od zmiennych ψa+ψb i ψa-ψb:


Na podstawie równości (1.85) otrzymujemy pierwsze równanie na kwadrat częstotliwości kołowej drgań (1.77), a także z równania (1.86) wynika drugi kwadrat częstotliwości kołowej drgań normalnych (1.82). Z równań (1.85) i (1.86) wnioskujemy, że można napisać następujące dwa równania:


Całkowite rozwiązanie ruchu opisujące przez równanie (1.87) i równanie (1.88) są opisywane dla Ψa:

A także rozwiązanie opisujące ruch ciała drugiego jest opisywane:

Drgania poprzeczne, układ sprężynek i ciężarków[edytuj]
Rozważmy teraz sobie konfigurację sprężynek wykonujących drgania poprzeczne. Rozpatrzmy teraz konfigurację, w którym środkowa sprężynka nie jest wcale naprężona, wtedy równanie ruchu pierwszej masy przestawiamy:

Równanie ruchu drugiego ciała jest bardzo podobne do (1.91). To równanie rozwiązuje się tak samo jak (1.16) pamiętając przy tym o (1.15), zatem kwadrat częstotliwości kołowej opisujący pierwsze drganie normalne dla ψa=ψb liczymy według:

Następną postacią drgań normalnych jest to drganie, którego dla tego ruchu zachodzi ψA=-ψb, kąt pomiędzy sprężynką pierwszą a poziomem jest dwukrotnie mniejszy niż kąt pomiędzy sprężynką drugą a poziomem, co będziemy korzystali w wyprowadzeniu równania ruchu dla drugiej postaci drgań normalnych:

Równanie ruchu dla drugiej sprężynki jest bardzo podobne do (1.93). Równanie (1.93) rozwiązuje się bardzo podobnie jak równanie (1.16) pamiętając przy okazji o (1.15), zatem kwadrat częstotliwości drgań normalnych możemy przestawić:

Dwa sprzężone ze sobą obwody LC[edytuj]
Układ dwóch sprzężonych ze sobą obwodów LC nazywamy układ składający się z trzech kondensatorów o pojemności C równoległych względem siebie i dwóch cewek o indukcyjności własnej L też równoległych wobec siebie. Napiszmy teraz równania różniczkowe według drugiego prawa Kirchhoffa, które rządzą dwoma oczkami z osobna, które to powiązane są ze sobą względem prądów płynących przez cewki Ia i Ib, i przy pomocy ładunków znajdujących się na poszczególnych kondensatorach Q1, Q2 i Q3:


Możemy z różniczkować równania (1.95) i (1.96) względem czasu i w ten sposób otrzymujemy stąd dwie dalsze tożsamości zawierające prądy Ia, Ib, a także pochodnych ładunków znajdujących się na kondensatorach Q1, Q2, Q3 policzonych względem czasu:


Z pierwszego prawa Kirchhoffa możemy otrzymać trzy tożsamości, które wiążą ładunki na kondensatorach z natężeniami prądów płynących w poszczególnych obwodach:



Tożsamości (1.99), (1.100) i (1.101) możemy podstawić do wzorów (1.97) i (1.98), w ten sposób otrzymujemy dwie równości różniczkowe zależne od zmiennych Ia i Ib i od pozostałych parametrów:


Równania (1.102) i (1.103) możemy do siebie dodać i odjąć, w ten sposób otrzymać dwa równania zależne od zmiennych Ia+Ib oraz od Ia-Ib z osobna, z których możemy wyznaczyć te wielkości w postaci ich drgań z pewnymi częstotliwościami kołowymi określonych kolejno przez ω1 i ω2, zatem te dwa równania piszemy jako:


Z równań (1.104) i (1.105) możemy otrzymać dwie wspomniane wcześniej częstotliwości kołowe drgań normalnych, której to kwadraty:


Układ drga z jedną częstotliwości kołowych, którego kwadraty są opisywane wzorami (1.106), (1.107), gdy dla pierwszej mamy Ia=Ib, a dla drugiej Ia=-IB. Ogólne rozwiązania na natężenia prądów Ia i Ib są zapisane jako:


Dudnienia[edytuj]
Jest wiele przykładów układów drgających z dwiema częstotliwościami podstawowymi ω1 i ω2, przykładem takich drgań mogą być drgania o dwóch stopniach swobody. Przykładem układów o dwóch stopniach swobody są drgania spowodowane przez dwie siły wymuszające drgających z dwoma częstotliwościami. Aby zobaczyć co to są dudnienia, rozpatrzmy dwa drania o takich samych amplitudach i różnych częstotliwościach podstawowych, które są opisane przez:


Całkowite wychylenie od położenia równowagi określamy jako sumę wychyleń (1.110) i (1.111) i są one zależne od częstotliwości kołowych ω1 i ω2:

Modulacje[edytuj]
Średnią częstotliwość kołową ωśr, która jest sumą częstotliwości kołowych ω1 i ω2 podzielonych przez dwa, oraz częstotliwość kołową modulacji ωmod, która jest różnicą dwóch częstotliwości kołowych podanych wcześniej i podzielonych przez dwa:


Częstotliwości drgań kołowych drgań normalnych możemy napisać w zależności od częstotliwości drgań średnich i częstotliwości drgań modulacji:


Jeszcze raz patrząc na wzór (1.112) przy takich samych amplitudach A i B, które tutaj oznaczymy przez A, a także na wzory (1.115) i (1.116), wtedy możemy dojść do wniosku:

- gdzie amplituda modulacyjna określamy według wzoru (1.117):

Wzór (1.117) jest wzorem ogólnym, ale największe korzyści daje nam, gdy częstotliwości ω1 i ω2 są do siebie zbliżone, to wtedy mamy na pewno ω1≈ω2 i ωmod<<ωsr, a więc amplituda praktycznie się nie zmienia i wtedy układ wykonuje drania prawie harmoniczne o częstości ωsr. Natomiast gdy ωmod=0, to wtedy mamy ωsr=ω1=ω2, jeśli te częstotliwości kołowe różnią się niewiele, to taki ruch nazywamy prawie harmonicznym lub prawie monochromatycznym o częstotliwości ωsr i o amplitudzie prawie się nie zmieniającej.
Dudnienia wywołane przez dwa kamertony[edytuj]
Rozważmy dwa kamertony, które wywołują fale dźwiękowe, które powodują zmiany ciśnienia w pobliżu błony bębenkowej, której jako ψ jest różnicą ciśnień błony bębenkowej pomiędzy jej warstwą zewnętrzną a wewnętrzną. Jeśli mamy dwa kamertony, to ta różnica na naszej błonie jest równa sumie różnic ciśnień ψa+ψb, czyli jest superpozycją dwóch fal pochodzących od kamertonów. Gdy różnica częstotliwości ν różnią się o więcej niż 6%, to nasz mózg, wolą opis drgań opisany wzorem (1.112). Oznacza to, że fale o dwóch częstotliwościach są słyszane jako dwa odrębne dźwięki. Jeśli natomiast mamy 

Detektor mocy superpozycji fali dźwiękowej[edytuj]
Według wzoru (1.118) amplituda fali dźwiękowej oscyluje z częstością kołową modulacji ωmod, co za każdym razem ωmodt zwiększa się o 2π, w której amplituda modulacji Amod wykonuje pełny cykl modulacji (mamy tu na myśl powolne zmiany zmiany z częstotliwością modulacji ωmod). W tym czasie amplituda Amod dwa razy przyjmuje wartość równą zero, w której ludzkie ucho nic nie słyszy, a także przyjmuje dwa razy wartość bezwzględną równą wartości maksymalnej, tzn. raz maksymalną wartość wziętej z minusem, a za drugim razem z plusem, czyli w tym czasie amplituda przyjmuje dwa różne znaki o takiej samej wartości bezwzględnej amplitudy. Ludzkie ucho nie rozróżnia z jakim znakiem amplitudy mamy do czynienia, ale rozróżnia jedynie kwadrat amplitudy fali dźwiękowej, który ma dwa maksima w jednym trakcie okresu.

Częstością dudnień nazywamy częstość powtarzania się maksymalnego kwadratu amplitudy fali modulowanej, jest ona pisana wzorem:

Aby przekonać się o tym, że kwadrat amplitudy modulowanej, czyli kwadrat z (1.118) drga z częstotliwością kołową (1.119), to napiszmy następujące przekształcenia wykorzystując znane związki z trygonometrii, wtedy:

Widzimy na podstawie obliczeń (1.120), że kwadrat amplitudy oscyluje z podwojoną częstotliwością modulowaną (1.119), co było do wykazania.
Dudnienia słabo sprzężonych ze sobą wahadeł[edytuj]
Weźmy układ dwóch wahadeł słabo sprzężone ze sobą, czyli dwie masy M zawieszone na nieważkich niciach, oraz połączone ze sobą przy pomocy sprężynki o stałej sprężystości K. Rozwiązując równania ruchu dla tych mas M, dowiemy się, że układ może drgać z dwiema częstotliwościami kołowymi, które są opisywane w zależności od stałej sprężystości K, przyspieszenia grawitacyjnego g i masy M. Mając równania ruchu możemy określić częstotliwości dudnień lub częstotliwość modulowaną, a także częstotliwość średnią. Napiszmy teraz równania ruchu obu kulek w sposób:


Różniczkowe równania ruchu dla obu kulek M, tzn. (1.121) I (1.122) możemy dodać i odjąć od siebie, w ten sposób otrzymać wnioski zależne od zmiennych ψa+ψb (pierwsza równość) i od ψa-ψb (druga równość), by z tych równań wyznaczyć wzory na wspomniane zmienne przy pomocy definicji częstotliwości ω1 i ω2:


Patrząc na wzory (1.123) i (1.124), w ten sposób otrzymujemy formuły na kwadraty wspomnianych częstotliwości kołowych drgań harmonicznych, których przedstawienie jest zależne od przyspieszenia ziemskiego "g", długości wahadła matematycznego "l" i stałej sprężystości K i masy obu kulek M:


W celu określenia jak wyglądają dudnienia napiszmy, czemu są równe ψa I ψb dla osobnych drgań harmonicznych, to napiszmy równania na przemieszczenie ciała "a" dla ψa i ciała "b" dla ψb przy definicji częstotliwości kołowych ω1 i ω2, w takim wypadku piszemy je:


Najsilniejszy efekt obserwuje się, gdy obie amplitudy są jednakowego znaku, tzn. A1=A2=A. Jeśli któraś z amplitud jest równe zero lub w przybliżeniu równe zero, to mamy do czynienia z drganiami harmonicznymi z drgających z jedną częstotliwością kołową, tzn. ω1 i ω2. Drgania dwóch mas przy jednakowych amplitudach możemy zapisać:


Wykorzystamy wzory (1.115) i (1.116), by potem je użyć do (1.129) (1.130), by dalej przeprowadzić końcowe obliczenia na drgania obu mas. Dla pierwszej masy mamy według wzoru na przemieszczenia ciała "a", czyli ψa (1.129):

Dla drugiej masy mamy według wzoru na przemieszczenia ciała "b", czyli ψb (1.130):

Energię kulki pierwszej określamy w zależności od częstotliwości modulacyjnej ωmod i ωsr, które określamy względem częstotliwości drgań podstawowych, którego piszemy przy pomocy kwadratu funkcji kosinus z iloczynu częstotliwości modulowanej i czasu, i częstotliwości średniej:

A energię drugiej kulki podobnie jak dla pierwszej kulki określamy przez:

Określmy teraz wielkość zwaną E, która jest sumą całkowitych energii kulki pierwszej (1.133) i drugiej (1.134), którego ta energia jest wielkością stałą jak można udowodnić, tzn. tylko zależy od częstotliwości średniej obu drgań podstawowych:

Całkowite energie kulki pierwszej (1.133) i drugiej (1.134), wykorzystując przy tym fakt (1.135), są napisane jako z definicji kwadratu sinusa i kosinusa kąta połówkowego:
![{\displaystyle E_{a}={{1} \over {2}}E\left[1+\cos(\omega _{1}-\omega _{2})t\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5b696a5fd03188bbd04b234c25a2dea89120c17)
![{\displaystyle E_{b}={{1} \over {2}}E\left[1-\cos(\omega _{1}-\omega _{2})t\right]\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd54c150bf9a035301b91806e4bc7043d1a14243)
A różnica energii obu kulek, tzn. Ea i Eb na podstawie (1.136) i (1.137) przestawiamy jako funkcję wprost proporcjonalną do kosinusa z argumentu (ω1-ω2)t, i wyrażamy ją: