Liczby zespolone/Argument liczby

Argument liczby zespolonej

Znając już definicję modułu liczby zespolonej - jej odległości od początku układu współrzędnych, możemy liczby zespolone opisać nie tylko za pomocą punktów - ale również za pomocą, wspomnianego we wcześniejszych rozdziałach, wektora o początku w punkcie (0,0) i końcu w punkcie o współrzędnych liczby zespolonej. A długość tego wektora będzie równa modułowi liczby zespolonej.

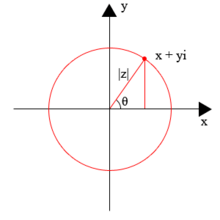
Znając moduł liczby zespolonej, możemy jedynie wykreślić okrąg na którym znajdować się będzie nasza szukana liczba.

Z twierdzenia sinusów i cosinusów - możemy wyznaczyć kąt, nachylenia wektora

Argrand zauważył, że znając moduł liczby zespolonej - można by spróbować tym parametrem opisać jej wartość. Jednak dla pewnych punktów odległość od początku układu współrzędnych płaszczyzny zespolonej będzie taka sama. O ile dla liczb rzeczywistych moduł określał wartości tylko dwóch liczb (dodatniej i jej przeciwnej), to w przypadku płaszczyzny zespolonej wodząc wektorem o znanej długości zakreślimy okrąg o promieniu $r=|z|\!$ - punktów będzie nieskończenie wiele. Potrzebny więc będzie jeszcze jeden argument - jakaś dodatkowa współrzędna. Najlepiej, ogólnie akceptowalna, znana i łatwo otrzymywana w sposób przypominający dotychczas znane działania.

Argrand rozrysowując wektor wpadł na pomysł, w jaki sposób, znając już moduł liczby $|z|\!$ , tylko jednym dodatkowym argumentem precyzyjnie określić położenie na płaszczyźnie zespolonej. W tym przypadku, wykorzystał ponownie własności trójkąta prostokątnego oraz twierdzenie cosinusów i twierdzenie sinusów, znanych z kartezjańskiego układu współrzędnych. Dzięki nim można było wyznaczyć kąt $\varphi \!$ pomiędzy wektorem opisującym liczbę oraz osią rzeczywistą Re. Kąt ten należy do zbioru liczb rzeczywistych: $\varphi \in \mathbb {R}$ i nazywany jest argumentem liczby zespolonej.

Z obu twierdzeń, cosinusów i sinusów, Argrand wyprowadził zależności, pozwalające określić argument liczby zespolonej:

{\begin{cases}\operatorname {cos} \left(\varphi \right)={\frac {a}{|z|}},\\\operatorname {sin} \left(\varphi \right)={\frac {b}{|z|}}.\end{cases}}

Oczywiście, wartość kąta może być znaczna - wodząc wektorem po okręgu, możemy wykonać wiele okrążeń. Dlatego ustalono, że argument główny liczby zespolonej powinien mieścić się w przedziale wartości od 0° do 360° - aby nie zmuszać ludzi do zbędnego wykonywania przeliczeń i wodzenia po okręgu. Obecnie, w dobie skomputeryzowania, miara kątowa uznana jest za archaiczną i wartości kątów podawane są w radianach. Stąd argumentem głównym liczby zespolonej $z\neq 0$ nazywamy kąt ograniczony: $0\leq \varphi <2\pi$ .

Liczbę zespoloną $z=a+bi\!$ w płaszczyźnie zespolonej przedstawić można było do tej pory jako punkt - współrzędne miejsc zerowych $(a,b)\!$ - podając na podstawie miejsc zerowych jego współrzędne na osi liczb rzeczywistych Re oraz na osi liczb urojonych Im. Dzięki zabiegom Argranda, od teraz liczby zespolone można przedstawiać również podając ich współrzędne biegunowe $(|z|,\varphi )\!$ .

Przejście z jednego układu współrzędnych do drugiego w matematyce nazwane jest transformacją. W celu transformacji pomiędzy oboma poznanymi układami używamy własności funkcji trygonometrycznych.