Liczby zespolone/Liczby zespolone
Liczby zespolone
[edytuj]| Liczbą zespoloną nazywamy uporządkowaną parę liczb rzeczywistych będących współrzędnymi tej liczby w przestrzeni (płaszczyźnie) liczb zespolonych. |
Ze względu na sposób rozpięcia przestrzeni (płaszczyzny) - liczby zespolone, jak nazwa wskazuje, są złożone: z części określającej położenie na osi rzeczywistej oraz urojonej . W roku 1833 William Hamilton (1805-1865) stwierdził, że skoro liczby rzeczywiste w kartezjańskim układzie współrzędnych można było zapisywać w postaci pary współrzędnych (x,y), to czemu nie zastosować tego sposobu dla liczb zespolonych?
- Stąd powstał:
| Zbiór liczb zespolonych oznaczamy literą : |
Zbiór wszystkich liczb zespolonych będzie więc rozpięty w opisanej wcześniej płaszczyźnie liczb zespolonych, której początkiem jest punkt .
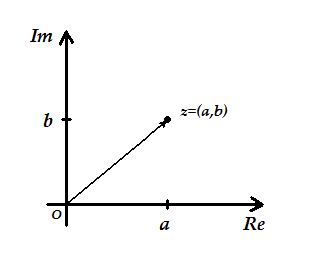
Liczbę zespoloną na płaszczyźnie przedstawia się tak, jak robiło się to z punktami innych układów dwuwymiarowych: w postaci punktu o współrzędnych (a,b) lub w postaci wektora o początku w punkcie O(0,0) i końcu w (a,b).
Jak szybko zauważymy, wszystkie liczby typu będą położone na osi Re - stąd wniosek że możemy je utożsamiać z liczbami rzeczywistymi. Natomiast wszystkie liczby odnajdziemy na osi Im - są liczbami urojonymi.
Mając już zdefiniowaną liczbę zespoloną, warto jest zastanowić się nad własnościami tych liczb. W podręczniku nieustannie powtarzamy, że liczby zespolone to twory matematyczne mające uzupełnić przestrzeń liczb rzeczywistych - toteż poddane różnego rodzaju operacjom powinny się one poniekąd zachowywać podobnie. Toteż poniżej wypisano własności liczb zespolonych.
Własności liczb zespolonych
[edytuj]Dowolne liczby zespolone w określonych przypadkach podstawowych działań matematycznych wykazują własności:
- nie reagują w dodawaniu z zerem:
- ,
- nie reagują w mnożeniu z 1, liczbą :
- ,
- liczba przeciwna do to :
- ,
- przemienność dodawania:
- ,
- łączność dodawania:
- ,
- przemienność mnożenia:
- ,
- łączność mnożenia:
- ,
- rozdzielność mnożenia względem dodawania:
- liczba odwrotna do to :
- ,