Liczby zespolone/Postać algebraiczna
Postać algebraiczna
[edytuj]Wróćmy jednak do liczb rzeczywistych i przypomnijmy sobie rozważania na temat pierwiastków liczb ujemnych otrzymywanych przy rozwiązywaniu równań kwadratowych. Liczby te miały nieporęczną postać sumy pewnej liczby rzeczywistej z pierwiastkiem liczby ujemnej.
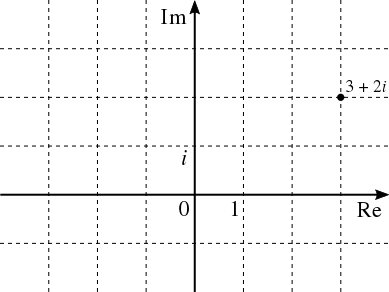
Po wprowadzeniu jednostki urojonej i postać ta stała się bardziej klarowna - jednoznacznie określała bowiem rozdzielność obu typów liczb, w sposób zbliżony do popularnego do dziś sposobu realizacji równań funkcji 2 zmiennych X i Y w układzie kartezjańskim. Szybko zauważymy, że zmieniając wartości rzeczywiste na osi Re, liczba zespolona z na płaszczyźnie przesunie się jedynie w poziomie bez zmian w części urojonej - i na odwrót: zmieniając parametry na osi urojonej Im liczba zespolona przesunie się na wykresie jedynie w pionie, bez zmian części rzeczywistej. Przykładowo jeśli znajdując na osi rzeczywistej liczbę a=3 dodamy do niej liczbę urojoną bi=2i znajdziemy się w punkcie liczby zespolonej o współrzędnych .
Stąd też jeśli a jest częścią rzeczywistą liczby z określoną jako Re(z), oraz b cześcią urojoną liczby zespolonej określaną jako Im(z) to:
- z = Re(z) + Im(z)·i
Każdą liczbę zespoloną można więc przedstawić w postaci algebraicznej:
| liczbę rzeczywistą a nazywamy częścią rzeczywistą liczby zespolonej z, i zapisujemy jako Re(z)=a; liczbę b nazywamy częścią urojoną liczby zespolonej z, i zapisujemy jako Im(z)=b; |
Poprzednią definicję zbioru liczb zespolonych możemy więc rozszerzyć o stwierdzenie że:
| Zbiór liczb zespolonych oznaczamy literą :
|
Obie te postaci są ze sobą równoważne i są ściśle ze sobą związane.
Warto również zauważyć, że liczby postaci lub (0,b), gdzie z pominięciem zera - punktu (0,0), zwykło nazywać się czysto urojonymi (0 jest liczbą rzeczywistą).













