Matematyka dla liceum/Funkcja liniowa/Wykres i własności

Wykres funkcji liniowej

Wykresem funkcji liniowej jest prosta. Aby narysować wykres funkcji liniowej, wystarczy wyznaczyć współrzędne dowolnych dwóch punktów tej funkcji i poprowadzić przez nie prostą.

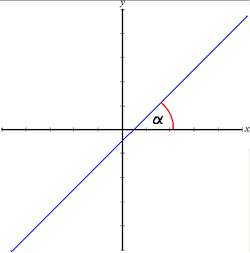
Prosta, która jest wykresem funkcji y=ax+b, nachylona jest do osi OX pod takim kątem, że

$a=tg\alpha \qquad \alpha \in (0,{\tfrac {\pi }{2}})\cup ({\tfrac {\pi }{2}},\pi )$

gdzie: a to współczynnik przy x, $\alpha$ to kąt między prostą a osią OX

Prosta przecina oś OY w punkcie (0,b) oraz oś OX w punkcie (-b/a, 0) – można to łatwo wyznaczyć z jej wzoru, y=ax+b (podstawiając 0 za y lub za x).

TWIERDZENIE Wykresem funkcji liniowej $f(x)=ax$ jest prosta przechodząca przez początek układu współrzędnych o współczynniku kierunkowym a. Wykresem funkcji liniowej $f(x)=ax+b$ jest prosta przechodząca przez punkt (0;b) o współczynniku kierunkowym a.

Własności funkcji liniowej

Dziedziną funkcji liniowej jest zbiór wszystkich liczb rzeczywistych R.

Miejsce zerowe funkcji jest punktem, w którym funkcja przecina oś OX, oblicza się je z  $x_{0}=-{\tfrac {b}{a}}$

Monotoniczność funkcji liniowej

• $a>0\,$ funkcja rosnąca
• $a<0\,$ funkcja malejąca
• $a=0\,$ funkcja stała

Przykład
Funkcja $y=-3x+1$ jest malejąca.

Parzystość
Funkcja jest parzysta, gdy $a=0\,$ (funkcja stała).
Funkcja jest nieparzysta, gdy $b=0\,$ (przechodzi przez środek układu wsp.) i $a\neq 0$.

Różnowartościowość
Funkcja jest różnowartościowa, jeśli $a\neq 0$, w przeciwnym wypadku nie jest różnowartościowa (jest stała i zawsze przyjmuje tę samą wartość).

Okresowość
$a\neq 0\,$ funkcja nie jest okresowa.
$a=0\,$ funkcja jest okresowa (stała), jej okresem jest każda liczba R.

Wykresy dwóch funkcji
Jeśli porównać wykresy dwóch funkcji, to mogą one być:

• równoległe, gdy $a_{1}=a_{2}$ – oba współczynniki są równe
• prostopadłe, gdy $a_{1}={\tfrac {-1}{a_{2}}}$

Przykład
Wykresy funkcji: $f(x)=3x+1$ i $g(x)=3x-7$ są liniami równoległymi do siebie.