Wstęp do fizyki cząstek elementarnych/Teoria oddziaływań i pól kwantowych
Licencja
|
|---|
|
Autor: Mirosław Makowiecki
Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność. |
Podręcznik: Wstęp do fizyki cząstek elementarnych.
W teorii oddziaływania przyjmuje się, że oddziaływania są wynikiem wymiany między sobą bozonów, to musi odbywać się w czasie krótszym niż Δt określonym przez równanie 
Teoria pól kwantowych Yukawy
[edytuj]Poszukując krótkozasięgowe oddziaływanie pomiędzy protonami, a neutronami w jądrach, można opisywać bezpośrednio za pomocą równania kwantowego Kleina-Gordona:

Gdy będziemy rozpatrywać będziemy pola bez udziału czasu, i zakładając, że funkcja jest zależna tylko od od "r":

Pamiętając, że zachodzi (2.1), a także (2.2), to wtedy na podstawie tego zależność potencjału od "r" i od stałej g0, jest w postaci:

Wyznaczmy pierwszą pochodną wyrażenia (2.3) względem "r" w zależności od parametru g0, m0 i 

Następnym krokiem jest policzenie pochodnej względem "r" podzielonej przez r2 iloczynu kwadratu "r" i pochodnej cząstkowej wielkości U(r) względem "r":


wtedy równanie (2.1) dla przypadku stacjonarnego po działaniu operatorem Δ funkcję U(r), czyli (2.5), stąd rozwiązaniem (2.1) jest (2.3).
Transformata pędu cząstki
[edytuj]Napiszmy ile wynosi transformata Fouriera cząstki potencjału 



![{\displaystyle =g_{0}g{{\hbar } \over {2iq}}\int _{0}^{\infty }dre^{-{{r} \over {R}}}\left(e^{i{{qr} \over {\hbar }}}-e^{-i{{qr} \over {\hbar }}}\right)=g_{0}g{{\hbar } \over {2iq}}\int _{0}^{\infty }\left[e^{r\left(-{{1} \over {R}}+i{{q} \over {\hbar }}\right)}-e^{-r\left({{1} \over {R}}+i{{q} \over {\hbar }}\right)}\right]=\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864aa00404608b7ebddbd0c44745a7c3b35389c4)


Powyższa dyskusja dotyczy rozpraszania cząstki o stałej sprzężenia g opisanej równaniem (2.6) dla potencjału U(r) zależnej tylko od promienia położenia cząstki na danym potencjale i niezależnej od współrzędnych cząstkowych. U(r) jest to pole statyczne. Propagacja bozonu opisuje rozpraszanie elastyczne na danym potencjale. Proces wymiany dwóch bozonów dla przypadków opisujących cząstkę rozpraszającą a cząstką rozpraszaną propagator bozonu jest iloczynem stałych sprzężenia g i g0 przez sumę kwadratów m0c i q.
Opis podstawowych oddziaływań w przyrodzie
[edytuj]Oddziaływania elektromagnetyczne
[edytuj]Stała sprzężenia, która charakteryzuje cząstki ze sobą oddziaływających piszemy w zależności od ładunku elektronu, stałej prędkości światła, stałej Planka i nazwiemy ją stała struktury subtelnej:

Ona określa rozszczepienie widm atomowych oddziaływań spin-orbita. Pola elektromagnetyczne mogą być transformowane jak wektory i dlatego foton. który jest przekaźnikiem oddziaływania jest cząstką wektorową. Jeśli będziemy definiować moment magnetyczny jako:

gdzie s=1/2, w teorii Diraca (mechanice kwantowej) otrzymujemy g=2. Weźmy ile jest równa wielkość g w elektrodynamice kwantowej jako wielkość odchylenia od liczby g.

Bardzo ważną teorią jest elektrodynamika kwantowa QED. Ta owa teoria opisuje właściwości zwane renormalizowalnością i niezmienniczością względem cechowania.
Rysunek obok przedstawia pojedynczy elektron, który oddziaływuje sam ze sobą poprzez fotony wirtualne lub ona przedstawia wirtualną parę cząstek elektron-pozyton. Linie elektronowe dla diagramach Feymanna reprezentuje sam "goły" elektron ubrany w procesy, które stanowią procesy wirtualne poprzez wymianę fotonów wirtualnych. Ograniczenia na pęd "k" nie ma. W teorii QED występują rozbieżne całki, które można zastąpić predyfiniując ładunek i masę, który zawsze występuje w obliczeniach z czynnikiem multiplikatywnym, która posiada całkę rozbieżną. Zatem te dwa ładunki można zastąpić przez wielkości mierzone doświadczalnie, tzn. e i m. Taki stan postępowania nazywamy renormalizacją. Okazuje się, że QED stała sprzężenia wcale nie jest stałą, tylko zależy w skali logarytmicznie od energii w dokonywanym procesie. Bardzo ważnym elementem jest niezmienniczość względem cechowania, co jest ważne do teorii renormalizowalności. Dla rzędu skali energii Z0 współczynnik sprzężenia wynosi 1/128, a nie 1/127.
Oddziaływanie silne
[edytuj]Rozpatrzmy cząstkę Σ0(uds), która rozpadać się może na cząstki Λ i γ, a silne rozpady tej cząstki są zabronione, ze względu na zasadę zachowania izospinu, a Λ jest stanem singletowym i ma spin 1/2, natomiast na rozkład Λ i π0 zachodzi z oddziaływaniem silnym, dalej cząstka Σ+ są barionami o spinie 1/2 i jej rozkład może zachodzić z użyciem oddziaływania silnego.
| Barion | Skład | Wartość energii rozpadu Q [MeV] | Sposoby rozpadu | Czas życia [s] |
|---|---|---|---|---|
| Σ0 | uds | 74 | 
|
10-19 |
| Σ0 | uds | 208 | 
|
10-23 |
| Σ+ | uus | 189 | 
|
10-10 |

Oddziaływanie silnie spotykamy w oddziaływaniach pomiędzy neutronami i protonami, a także pomiędzy kwarkami. Stosunek stałej sprzężenia oddziaływania silnego przez stałą sprzężenia oddziaływania elektromagnetycznego jak udowodnimy jest równy w przybliżeniu sto, czyli:

Ale ponieważ stała sprzężenia w oddziaływaniu elektromagnetycznym jest równa (2.7), zatem stała sprzężenia oddziaływania silnego jest równa w przybliżeniu jeden (αs≈1). Oddziaływania pomiędzy kwarkami w oddziaływaniu silnym zachodzi poprzez wymianę gluonu, który jest obojętny elektrycznie, jest ona cząstką wektorową o parzystości Jp=1-. W teorii oddziaływania między kwarkami istnieje 6 typów silnych ładunków kolorowych, przy czym każdy kwark niesie jeden ładunek kolorowy, czyli czerwony, zielony i niebieski, a antykwark odpowiednio antykolory. Sam gluon jest również obdarzony ładunkiem kolorowym, i dlatego one mogą bezpośrednio oddziaływać. W teorii QED istnieją sprzężenia pomiędzy bozonami przenoszących oddziaływanie, co jest charakterystyczne dla teorii nieabelowych, a elektrodynamika kwantowa jest teorią abelową. Gluony przenoszą jednocześnie ładunek kolorowy i antykolorowy, a tych kombinacji jest 32=9. Istnieje osiem stanów gluonowych, tzn. 

Oszacowaliśmy że αs, które odpowiadają wymianie jednego gluonu, a za wymiany wielogluonowe odpowiedzialne są kolejne człony potęgi stałych sprzężenia oddziaływania silnego. Potencjał pola silnego zależny od "r", a także od "k" i od stałej sprzężenia αs piszemy:

Pierwszy człon jest dominujący przy małych odległościach, a w przypadku drugim dla dużych odległości. Czynnik 4/3 w (2.11) jest uzasadniany tym, że mamy osiem stanów kolorowych, które uśredniamy po trzech stanach gluonowych. Drugi wyraz w (2.11) odpowiada z uwięzieniem kwarków w cząstkach elementarnych. Próby oderwania kwarku z cząstki elementarnej powoduje produkowanie nowych mezonów, za co jest odpowiedzialny drugi człon w potencjale na oddziaływanie silne. Podczas anihilacji elektronu i pozytonu, co wyniku której powstaje hadron, antyhadron, który jest fragmentacją kwarków.
Oddziaływanie słabe i elektrosłabe
[edytuj]Można zauważyć porównując rozpad zmieniający dziwność 


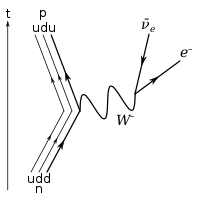
Przykładami oddziaływań z namiastką oddziaływania stałego są 


Dla q<<MW,Zc propagator oddziaływania słabego piszemy przy takim założeniu poprzez:

Oddziaływania grawitacyjne
[edytuj]Oddziaływania grawitacyjne nie grają żadnej roli w fizyce cząstek elementarnych. Jeżeli za jednostkę masy będziemy przyjmować mc2=1 GeV, to stała sprzężenia piszemy poprzez stałą grawitacji GN, stałą Planka kreśloną i prędkość światła, a także w zależności od masy źródła pola grawitacyjnego M, co w takowej sytuacji:

co porównując z stałą sprzężenia oddziaływania elektromagnetycznego (2.7). Dla mas zbliżonych do masy Planka 

Parametry oddziaływań w przyrodzie (Mc2=1 GeV)
[edytuj]W naszej tabeli przedstawimy wszystkie oddziaływania w przyrodzie grawitacyjne, elektromagnetyczne, słabe, silne. A także przedstawimy bozony pośredniczące w tych oddziaływaniach, spin i parzystość, zasięg, stałe sprzężenia, przekrój czynny, czas życia.
| Grawitatyjne | Elektromagnetyczne | Słabe | Silne | ||
|---|---|---|---|---|---|
| kwant pola | grawiton | foton | W± | Z | gluon |
| źródło | masa | ładunek elektryczny | ładunek słaby | ładunek kolorowy | |
| spin, parzystość | 2+ | 1- | 1- | 1+ | 1- |
| masa [GeV] | 0 | 0 | 80,2 | 91,2 | 0 |
| Zasięg [m] | ∞ | ∞ | 10-18 | ≤10-15 | |
| stała sprzężenia | 
|

|

|

| |
| Przekrój czynny | 10-33 | 10-39 | ≤10-30 | ||
| czas życia | 10-20 | 10-10 | 10-23 | ||
Przekroje czynne na zachodzące reakcje
[edytuj]Rozważmy reakcję, w której współuczestniczą dwa substraty a i b, wyniku której powstają dwa produkty c i d:

Miarą intensywności z jaką zachodzi dana reakcja jest przekrój czynny zachodzącej reakcji (2.15). Wiązka cząstek pocisku uderza w cząstki, które stanowią tarcze, czyli b, którego grubość jest dx, i koncentracja tych cząstek jest nb. Strumień, która przechodzi przez tarczę definiujemy jako iloczyn koncentracji cząstek a i prędkości vi, na jednostkę czasu:

Jeżeli przekrój czynny na zachodzenie reakcji jest σ, to prawdopodobieństwo zachodzenia reakcji jest σnbdx. A ilość reakcji zachodzącej w przekroju dx jest: φσnbdx. Prawdopodobieństwo, że reakcja będzie zachodziła jest W=φσ. Jednostką przekroju czynnego jest 1b=10-28m2. Prawdopodobieństwo zajścia reakcji W wiedząc, że Mif jest to element macierzowy zachodzenia reakcji pomiędzy stanem początkowym, a końcowym stanem reakcji, co można otrzymać z rachunku zaburzeń (jest to całka 

Jeżeli ρf przedstawia ilość stanów końcowych, co można zapisać ją jako pochodną dN/dE, tą wielkość zapiszmy w zależności od pędu i objętości danego układu badanego, w której zachodzi reakcja:

Będziemy przyjmować, że przekrój czynny liczony jest dla objętości V=1 i jednostkowej koncentracji cząstek na, wtedy pochodna przekroju czynnego czynnego względem kąta bryłowego w układzie środka masy jest:

Z definicji energii całkowitej dwóch produktów reakcji (2.15) mamy 


Przekrój czynny różniczkowy zachodzącej reakcji (2.15) piszemy na podstawie wzoru (2.19) i (2.20) w sposób:

Jeżeli cząstki w stanie początkowym mają spiny sa i sb, a w stanie końcowym spiny sc i sd, wtedy liczba stanów dostępnych w stanie początkowym i końcowym jest:


Rezonanse podczas zderzenia cząstek i ich rozpady
[edytuj]Średni czas zycia danej cząstki niestabilnej określamy jako odwrotność wielkości W (2.17). Gdy mamy doczynienia z rozpadami silnymi to τ jest niemierzalnie krótkie, i pod tym względem posługujemy się wielkością Γ, która jest szerokością (rozmyciem energii stanu podstawowego):

Rozmycie stanu podstawowego definiujemy jako pochodna liczby cząstek A względem czasu przez liczbę cząstek NA pomnożonej ze znakiem ujemnej przez stałą kreśloną Plancka, z którego obliczymy liczbę cząstek A w zależności od czasu:

Jeżeli mamy kilka kanałów rozpadów, to szerokość energii rozmycia energii stanu podstawowego jest sumą rozmycia poszczególnych energii stanu podstawowych poszczególnych kanałów reakcji. Γ=ΣiΓi. Stanu o dużej szerokości są to stany zwane rezonansami. Równość (2.25) określa kształt rezonansu. Funkcja falowa stanu niestabilnego, którego częstotliwość kołowa jest 

Policzmy teraz transfcrmatę funkcji (2.26) względem czasu:

Prawdopodobieństwo rezonansu utworzenia stanu z cząstek a i b jest wprost proporcjonalne do χ*(E)χ(E), zatem na tej podstawie (2.27) określamy wzorami:

Jak można zauważyć, przekrój czynny maleje do połowy swej wartości w przypadku wzoru (2.28), gdy zachodzi E-ER=±Γ/2. Fala płaska jest sumą poszczególnych fal o różnych orbitalnych liczbach kwantowych 


![{\displaystyle \sigma =\pi \left(b_{l+1}^{2}-b_{l}^{2}\right)=\pi \not {\lambda }^{2}\left[(l+1)^{2}-l^{2}\right]=\pi \not {\lambda }^{2}\left[l^{1}+2l+1-l^{2}\right]=\pi \not {\lambda }^{2}(2l+1)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ef043acff66201d960330a6e7e4290f6ca93895)
Amplituda na rozpraszanie elastyczne maksymalne jest dwukrotne większe niż (2.29), zatem na podstawie wcześniejszych rozważań i (2.28) uwzględniając krotność wynikająca ze stanów spinowych ,mamy:

Rezonanse Δ++ w układzie zderzeniowym π+ (pion) i p (proton)
[edytuj]Utworzenie cząstki Δ++ w wyniku zderzenia pionu i protonu, która po pewnej chwili rozpada się na takie same cząstki z jakich został utworzony, ono zachodzi według:

Cząstka Δ++ ma spin J=3/2, szerokość Γ=120 MeV, a także spiny sa=sb=1/2 i sb=sπ=0. Przekrój czynny na utworzenie tego stanu dla przypadku rozpraszania elastycznego jest 
Rezonans na utworzenie stanu Z0
[edytuj]Jest to bozon pośredniczący w oddziaływaniu słabym, jego wartość centralna masy jest 91 GeV, a jego szerokość rezonansu jest Γ=2,5 GeV. Bozon Z0 może się rozpaść na hadrony tworząc parę 



a także również na parę leptonów obojętnych:




