Matematyka dla liceum/Funkcje i ich własności/Inne własności funkcji

Dla funkcji możemy określić zbiór tych argumentów, dla których funkcja jest dodatnia, a także zbiór tych argumentów, dla których funkcja jest ujemna.

Różnowartościowość funkcji

DEFINICJA Funkcja $f: X \rightarrow Y$ jest różnowartościowa wtedy i tylko wtedy, gdy funkcja ta różnym argumentom przyporządkowuje różne wartości. $\forall_{x_1, x_2 \in X \and x_1 \neq x_2} f(x_1) \neq f(x_2)$

Przykład 1. Funkcja $f(x)=x$ jest różnowartościowa, co łatwo zauważyć na wykresie. Żadne dwa punkty należące do wykresu, nie są na tej samej wysokości (nie mają takiej samej współrzędnej y).

Różnowartościowość tej funkcji wynika także z tego, że jest to funkcja rosnąca.

Przykład 2. Poniższa funkcja także jest różnowartościowa.

Zauważmy, że jeśli funkcja jest rosnąca lub malejąca, to jest także różnowartościowa.

Przykład 3. Poniższa funkcja nie jest różnowartościowa. Możemy zauważyć, że dla argumentów $x = 1$ oraz $x = -1$ przyjmuje ona taką samą wartość równą 1.

Nieróżnowartościowość funkcji jest związana z istnieniem ekstremum, w którym funkcja zmienia swą monotoniczność z malejącej na rosnącą.

Parzystość i nieparzystość funkcji

DEFINICJA Funkcję f nazywamy parzystą wtedy i tylko wtedy, gdy dla każdej liczby x należącej do dziedziny funkcji, liczba przeciwna -x również należy do dziedziny tej funkcji oraz zachodzi $f(x)=f(-x)$. $\forall x \in D_f: -x \in D_f \and f(x)=f(-x)$

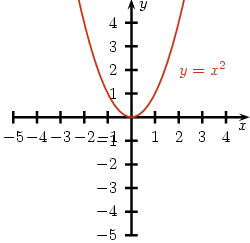
Przykład 1. Funkcja $f(x)=x^2$ jest parzysta, ponieważ $f(x)=x^2=(-1)^2x^2=(-x)^2=f(-x)$ i $x \in D_f \mbox{ oraz } -x \in D_f$, zatem spełnia warunki określone w definicji.

Zobaczmy teraz na wykres:

Zauważmy, że funkcja jest parzysta jeśli jest symetryczna względem osi OY.

Przykład 2. Funkcja $f(x) = |x|$ jest parzysta, ze względu na to, że zachodzi $f(x) = |x| = |-x| = f(-x)$. Poza tym widzimy symetrię na wykresie funkcji.

DEFINICJA Funkcję f nazywamy nieparzystą wtedy i tylko wtedy, gdy dla każdej liczby x należącej do dziedziny funkcji, liczba przeciwna -x również należy do dziedziny tej funkcji oraz zachodzi równość $-f(x)=f(-x)$. $\forall x \in D_f: -x \in D_f \and -f(x)=f(-x)$

Funkcja nieparzysta jest symetryczna względem punktu (0,0).

Przykład 3. Funkcja $f(x)=3x$ jest nieparzysta, ponieważ $-f(x)=-3x=3(-x)=f(-x)$

Przykład 4. Funkcja $f(x) = x^3$ jest nieparzysta.

Zachodzi $-f(x) = -x^3 = (-1)^3 \cdot x^3 = f(-x)$.

Okresowość

DEFINICJA Funkcję f nazywamy okresową wtedy i tylko wtedy, gdy istnieje taka liczba T różna od zera, że dla każdej liczby x należącej do dziedziny funkcji, liczby x+T oraz x-T również należą do dziedziny tej funkcji oraz zachodzi $f(x+T)=f(x)$. Liczba T nazywana jest okresem tej funkcji, a najmniejsza istniejąca taka liczba to okres podstawowy. $\exist_{T \neq 0} \forall_{x \in D_f} (x+T) \in D_f \and (x-T) \in D_f \and\ f(x+T)=f(x)$

Przykład 5.

Poniższa funkcja jest okresowa:

Okres podstawowy tej funkcji wynosi 2, ponieważ $f(x) = f(x+2)$.

Przykład 6.

Funkcja $y=\sin{x}$ jest funkcją okresową. Okres tej funkcji wynosi $2 \pi$.