Matematyka dla liceum/Funkcje i ich własności/Przekształcanie wykresu funkcji

przekształcanie wykresu funkcji

Do podstawowych przekształceń wykresu funkcji y = f(x) zaliczamy:

• symetrię względem osi X - otrzymujemy wtedy wykres funkcji y = - f(x)
• symetrię względem osi Y - otrzymujemy wtedy wykres funkcji y = f(-x)
• symetrię względem początku układu współrzędnych - otrzymujemy wtedy wykres funkcji y = - f(-x)
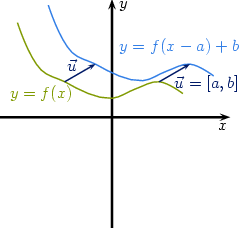
• translacja (przesunięcie) o wektor ${\vec {u}}=[a,b]$ - otrzymujemy wtedy wykres funkcji y = f(x - a) + b
• nałożenie wartości bezwzględnej
• zmiana skali

Symetria względem osi X

symetria względem osi OX

Jeśli punkt P(x,y) przekształcimy przez symetrię względem osi X, to otrzymamy punkt P'(x',y'), w którym x'=x a y'=-y. Jeśli daną funkcję przekształcimy przez symetrię względem osi X, to dla dowolnego punktu P(x,y) należącego do wykresu funkcji y=f(x) po przekształceniu otrzymamy punkt P'(x',y'), gdzie x'=x i y'=-y=-f(x)=-f(x'), Zatem wykres funkcji przekształconej poprzez symetrię względem osi X będzie miał wzór y=-f(x).

Przykład 1. Zapisz wzór funkcji f(x)=3x+5 w symetrii względem osi X.
y=-f(x)=-(3x+5)= -3x-5.

Przykład 2. Zapisz wzór funkcji f(x)=2log₃(x+2) w symetrii względem osi X.
y=-f(x)=-(2log₃(x+2))=-2log₃(x+2).

Symetria względem osi Y

symetria względem osi OY

Jeśli punkt P(x,y) przekształcimy przez symetrię względem osi OY, to otrzymamy punkt P'(x',y'), w którym x'=-x a y'=y. Jeśli daną funkcję przekształcimy przez symetrię względem osi Y, to dla dowolnego punktu P(x,y) należącego do wykresu funkcji y=f(x) po przekształceniu otrzymamy punkt P'(x',y'), gdzie x'=-x i y'=y=f(x)=f(-x'), Zatem wykres funkcji przekształconej poprzez symetrię względem osi Y będzie miał wzór y=f(-x).

Przykład 1. Zapisz wzór funkcji f(x)=3x+5 po przekształceniu przez symetrię względem osi OY.
y=f(-x)=3(-x)+5= -3x+5

Przykład 2. Zapisz wzór funkcji f(x)=2log₃(x+2) po przekształceniu przez symetrię względem osi OY.
y=f(-x)=2log₃(-x+2)

Symetria względem środka układu współrzędnych

symetria względem początku układu współrzędnych

Jeśli punkt P(x,y) przekształcimy przez symetrię względem początku układu współrzędnych, to otrzymamy punkt P'(x',y'), w którym x'=-x a y'=-y. Jeśli daną funkcję przekształcimy przez symetrię względem początku układu współrzędnych, to dla dowolnego punktu P(x,y) należącego do wykresu funkcji y=f(x) po przekształceniu otrzymamy punkt P'(x',y'), gdzie x'=-x i y'=-y=-f(x')=-f(-x), Zatem wykres funkcji przekształconej poprzez symetrię względem środka układu współrzędnych będzie miał wzór y=-f(-x).

Przykład 1. Zapisz wzór funkcji f(x)= -x³ po przekształceniu przez symetrię środkową względem środka układu współrzędnych- S_o.
y=-f(-x)=-(-(-x)³)=-x³.

Przykład 2. Zapisz wzór funkcji f(x)=2^xpo przekształceniu przez symetrię środkową względem środka układu współrzędnych - S_o.
y=-f(-x)=-2^(-x)=-2^-x=-$\left({\frac {1}{2}}\right)^{x}$ .

Translacja

translacja, przesunięcie funkcji

Jeśli punkt P(x,y) przekształcimy przez translację o wektor ${\vec {u}}=[a,b]$ to otrzymamy punkt P'(x',y'), w którym x'=x+a a y'=y+b. Jeśli daną funkcję przekształcimy przez translację o wektor ${\vec {u}}=[a,b]$, to dla dowolnego punktu P(x,y) należącego do wykresu funkcji y=f(x) po przekształceniu otrzymamy punkt P'(x',y'), gdzie x'=x+a i y'=y+b=f(x)+b=f(x'-a)+b, Zatem wykres funkcji przekształconej poprzez translację o wektor ${\vec {u}}=[a,b]$ będzie miał wzór y=f(x-a)+b.

Przykład 1. Zapisz wzór funkcji f(x)=2x² po przekształceniu przez translację o wektor ${\vec {u}}=[3,-2]$.
y=f(x-a)+b= 2(x-3)²-2.

Przykład 2. Zapisz wzór funkcji f(x)=log(x+2)-3 po przekształceniu przez translację o wektor ${\vec {u}}=[-3,5]$.
y=f(x-a)+b=log(x+3+2)+5-3=log(x+5)+2.

Nałożenie wartości bezwzględnej

nałożenie wartości bezwzględnej

Wykres funkcji $y=f(|x|)$ tworzymy poprzez usunięcie funkcji po lewej stronie osi OY i symetryczne odbicie prawej strony względem tej osi.

Wykres funkcji $y=|f(x)|$ tworzymy poprzez przełożenie części funkcji znajdującej się pod osią OX nad nią.