Matematyka dla liceum/Funkcje i ich własności/Zbiór wartości funkcji

Zbiór wartości funkcji

zbiór wartości funkcji, wyznaczanie zbioru wartości funkcji

DEFINICJA Zbiorem wartości funkcji nazywamy zbiór tych elementów zbioru Y, którym zostały przyporządkowane elementy ze zbioru X. Zbiór wartości funkcji f będziemy oznaczać przez $ZW_{f}$. $ZW_{f}=\left\{y\colon \exists _{x\in D_{f}}\ y=f(x)\right\}$

Zbiór wartości możemy także rozumieć jako zbiór wszystkich liczb (ściślej elementów zbioru Y), które zostały wyznaczone przez zrzutowanie jakiejś funkcji np. f na oś Y.

Przy wyznaczaniu zbioru wartości funkcji niejednokrotnie warto wykonać szkic funkcji. To prawie nic nie kosztuje, ale możemy na tym wiele zyskać. Poza tym osoba sprawdzająca rozwiązanie naszego zadania może uznać rysunek jako pewnego rodzaju dowód. Dlatego w większości podawanych przez nas przykładów będziemy rysować wykres funkcji, który w znacznej mierze może nam ułatwić znalezienie zbioru wartości funkcji, a sprawdzającym być może umili życie. Oczywiście nie należy popadać w skrajność, czasami spokojnie można pominąć rysunek, gdy rozwiązanie widać już na pierwszy rzut oka.

Zobaczmy na kilka przykładów:

Przykład 1. Mamy funkcję $f(x)=10$. Niezależnie, jakibyśmy wybrali x i tak f(x) będzie równe 10. Dlatego też $ZW_{f}=\{10\}$.

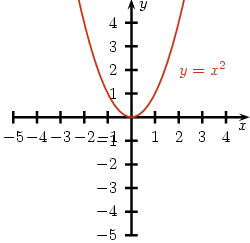
Przykład 2. Mamy funkcję $f(x)=x^{2}$. Wiemy, że funkcja ta przyjmuje wartości nieujemne, ponadto dla każdego $y\geq 0$ znajdziemy taki x, że $f(x)=y$ np. gdy weźmiemy $x={\sqrt {y}}$, wtedy $x^{2}=({\sqrt {y}})^{2}=y$. Tak więc $ZW_{f}=[0;+\infty )$. Nasze rozumowanie potwierdza rysunek.

Przykład 3. Wyznaczmy zbiór wartości funkcji $y=2-{\sqrt {2-2x}}$.

Pomyślmy... pierwiastek kwadratowy dowolnej liczby nigdy nie będzie ujemny, co najwyżej równy zero. Zatem najmniejsza wartość ${\sqrt {a}}$ wynosi zero, gdzie $a=2-2x$. Potem już dla większych a pierwiastek także staje się coraz większy np. dla ${\sqrt {400}}=20<{\sqrt {10000}}=100$. Zatem ${\sqrt {a}}$ dojdzie bardzo wysoko, bo aż do $+\infty$, czyli $ZW_{\sqrt {x}}=[0;+\infty )$. Ponadto od liczby 2 odejmujemy ten pierwiastek, zatem wszystko nam pójdzie „do góry nogami” przez znak „-” (czyli otrzymamy $(-\infty ;0]$), a następnie pójdzie o dwa „do góry” otrzymując $(-\infty ;2]$. Zatem $ZW=(-\infty ;2]$.

Jednak nie zawsze dopadnie nas natchnienie, wtedy musimy to zrobić w standardowy sposób:

• Wyznaczamy dziedzinę. Liczba podpierwiastkowa musi być nieujemna, zatem otrzymujemy nierówność $2-2x\geq 0$. Wykonując kilka przekształceń otrzymujemy $x\leq 1$.
• Rysujemy wykres funkcji uwzględniając dziedzinę. Sporządźmy w tym celu najpierw tabelkę:

x	-2	-1	0	1
y	$2-{\sqrt {6}}$	0	$2-{\sqrt {2}}$	2

Zatem wykres będzie podobny do tego:

• otrzymujemy, że $ZW=(-\infty ;2]$