Z Wikibooks, biblioteki wolnych podręczników.

Jest to wstępna wersja do druku. Podręcznik jest w trakcie tworzenia.

Jest to wersja do druku podręcznika Matematyka ubezpieczeń życiowych.

Jeśli widzisz tę informację to nie drukuj niczego! Kliknij na link Wersja do druku aby pozbyć się tej ramki, paska nawigacyjnego i innych niepotrzebnych elementów.
Kliknij Odśwież tę stronę przed wydrukowaniem, by wczytać najnowsze zmiany.
Więcej informacji o książkach do druku znajdziesz na stronie Wikibooks:Podręczniki do druku.

Matematyka ubezpieczeń życiowych

Aktualna, edytowalna wersja tego podręcznika jest dostępna w Wikibooks, bibliotece wolnych podręczników pod adresem
http://pl.wikibooks.org/wiki/Matematyka_ubezpiecze%C5%84_%C5%BCyciowych

Całość tekstu jest objęta licencją GNU Free Documentation License.

Spis treści

1 Wprowadzenie
2 Elementy teorii oprocentowania
- 2.1 Akumulacja i dyskontowanie
- 2.2 Renty
3 Model demograficzny
4 Podstawowe ubezpieczenia życiowe
5 Renty życiowe (Life annuities)
6 Składki netto (Net premiums)
- 6.1 Przykład
- 6.2 Funkcje komutacyjne w kalkulacji składek netto
7 Rezerwy składek netto (Net premium reserves)
8 Składki i rezerwy brutto
9 Wielorakie szkodowości (Multiple decrements)
- 9.1 Przypisy
10 Ubezpieczenia grupowe
11 Fundusze emerytalne
12 Literatura
- 12.1 Literatura
- 12.2 WWW

[edytuj] Wprowadzenie

Intencją niniejszego podręcznika jest dostarczenie czytelnikowi możliwie zwięzłego zestawienia podstawowych wiadomości z zakresu matematyki ubezpieczeń na życie. Z postulatu zwięzłości wynika pominięcie wielu wstępów teoretycznych, wyprowadzania wzorów i dowodzenia twierdzeń.

Kolejnym postulatem przyjętym przy tworzeniu tego opracowania było uporządkowanie i zestawienie wszelkich przydatnych wzorów w możliwie najłatwiejszej do zapamiętania postaci. Często więc zestawienia tabelaryczne będą dominować nad zredukowanymi do minimum objaśnieniami.

W zakresie doboru materiału wskazaniem są wymogi odnośnie egzaminów aktuarialnych. Wymagania te zostały przedstawione w dodatku.

Oprócz pozycji wymienionych w literaturze, jako istotne źródło informacji wymienić należy wykłady prof. dr hab. Bolesława Kacewicza na Wydziale Matematyki Stosowanej AGH w Krakowie (w roku 2002).

Ze względu na przyjęte założenia i ograniczenia, niniejszy podręcznik nie może zastąpić regularnych wykładów ani nie aspiruje do konkurowania z podręcznikami o ustalonej renomie na rynku.

Autor dokłada wszelkich starań by przedstawiane informacje były dokładne i odzwierciedlały rzeczywistą wiedzę z zakresu aktuariatu. Jeśli jednak w prezentowane tutaj treści wkradły się błędy, pomyłki lub nieścisłości to z tego miejsca kierowana jest gorąca zachęta do czytelnika by podjął się pomocy w ulepszeniu tego dzieła i naniósł poprawki osobiście lub choćby zwrócił na nie uwagę.

Kraków, 2008 r.

[edytuj] Elementy teorii oprocentowania

Niniejszy rozdział stanowi pewnego rodzaju elementarne wprowadzenie do zagadnień związanych z oprocentowaniem. W odróżnieniu od rozdziałów kolejnych dotyczyć on będzie sytuacji ściśle deterministycznych, pozbawionych czynnika losowego.

[edytuj] Akumulacja i dyskontowanie

Wszystkie procesy w niniejszym podręczniku będą mieć dwa modele - ciągły i dyskretny. Modele dyskretne będą oparte na wartościach poszczególnych wielkości w kolejnych latach lub podokresach lat.

[edytuj] Przypadek dyskretny

Rozpoczniemy od najprostszego przykładu lokaty terminowej na 1 rok. Na lokacie tej składamy na początku okresu jej trwania $k 0 = 1$ zł. Oprocentowana w skali rocznej dla tej lokaty jest w wysokości $i$ . Po roku otrzymamy więc

Czynnik $(1 + i)$ przez który musimy przemnożyć wyjściową kwotę nazywamy czynnikiem akumulującym, zaś liczbę $i$ nazywamy stopą oprocentowania i wyrażamy w procentach.

Jeśli zamiast podejmować pieniądze wznowimy tę lokatę to po $n$ latach otrzymamy

W powyższym rozumowaniu patrzyliśmy na początku inwestycji na to jaki będzie jej rezultat. Możemy odwrócić to rozumowanie i zapytać ile musimy zainwestować aby po $n$ latach uzyskać zadany kapitał. Odpowiedź uzyskujemy z prostego przekształcenia wzoru

Czynnik $\frac{1}{(1+i)}$ przez który (w odpowiedniej potędze) musimy pomnożyć $k n$ (kwotę którą chcemy uzyskać) nazywamy czynnikiem dyskontującym i oznaczamy literą $v$

Stopa oprocentowania $i$ dawała nam informację o ile procent więcej uzyskamy w wyniku inwestycji po 1 roku. Można teraz spytać inaczej. O ile procent mniejszą kwotą należało dysponować $1$ rok temu aby uzyskać obecną kwotę. Wartość ta jest oznaczana literą $d$ , wyrażana w procentach i nazywana stopą dyskontową

[edytuj] Przypadek ciągły

Przyzwyczajeni jesteśmy do myślenia o przepływie kapitału w sposób dyskretny (płatność jest dokonywana w konkretnym momencie czasu). W modelu ciągłym musimy zmienić nieco nasz sposób myślenia i postrzegać przepływ środków finansowych jako strumień o pewnej intensywności.

By to sobie uzmysłowić posłużymy się przykładem w którym pewną płatność za dany okres czasu będziemy dzielić na równe raty za coraz drobniejsze podokresy. Dokonując przejścia granicznego otrzymujemy nieskończenie wiele nieskończenie drobnych przepływów finansowych. Powyższy opis jakościowy ujmijmy teraz metodami ilościowymi. Tym razem posłużymy się przykładem inwestycji na okres jednego roku oraz inwestycji na podokresy roku. Przez $i (m)$ oznaczać będziemy nominalną stopę oprocentowania z kapitalizacją w podokresach długości $\frac{1}{m}$ roku. Równoważną takiemu składanemu oprocentowaniu stopę oprocentowania $i$ (za cały rok) otrzymamy z zależności

analogicznie dla stóp dyskontowych mamy:

Niech teraz $m$ dąży do nieskończoności. Wprowadźmy oznaczenie:

Wielkość ta jest nazywana intensywnością oprocentowania (ang. force of interest)

Łatwo zauważyć po zapisaniu zależności między $i (m)$ a $i$ w postaci

że $δ$ jest pochodną funkcji $(1 + i) x$ w punkcie $x = 0$ . Otrzymujemy więc zależność

Jaka jest jednak granica $d (m)$ ? Okazuje się, że taka sama. Łatwo bowiem pokazać, że

a stąd wykazuje się, że

Gdy oprocentowanie jest ciągłe różnica pomiędzy oprocentowaniem z góry i z dołu (czyli między akumulacją i dyskontowaniem) znika.

[edytuj] Podsumowanie

Zależności pomiędzy opisywanymi wielkościami ujmuje poniższa tabela

Nazwa	Oznaczenie	$i\,$	$d\,$	$v\,$	$\delta\,$
stopa oprocentowania	$i\,$	$-\,$	$i=\frac{d}{1-d}\,$	$i=\frac{1}{v}-1\,$	$i=e^{\delta}-1\,$
stopa dyskontowa	$d\,$	$d=\frac{i}{1+i}\,$	$-\,$	$d=1-v\,$	$d=1-e^{\delta}\,$
czynnik dyskontujący	$v\,$	$v=\frac{1}{1+i}\,$	$v=1-d\,$	$-\,$	$v=e^{-\delta}\,$
natężenie oprocentowania	$\delta\,$	$\delta=\ln(1+i)\,$	$\delta=\ln\frac{1}{1-d}\,$	$\delta=\ln\frac{1}{v}\,$	$-\,$
czynnik akumulujący		$1+i\,$	$\frac{1}{1-d}\,$	$\frac{1}{v}\,$	$e^{\delta}\,$

Najłatwiej przyswoić sobie powyższe wzory zapamiętując, że:

$v+d=1,\;$
$i\cdot v=d,\;$
$e^{\delta}=1+i.\;$

[edytuj] Renty

Renty w matematyce finansowej rozumiane są jako ciągi płatności. Będziemy posługiwali się wartościami obecnymi dla ciągów płatności jednostkowych. Mogą to być płatności dokonywane na początku lub na końcu roku przez pewną liczbę lat. W przypadku płatności na początku każdego roku przez $n$ , wartość obecną takich przepływów finansowych oznaczamy symbolem $\ddot{a}_{\overline{n}|}$ i jest ona równa

Po przekształceniu otrzymujemy:

Interpretacja: Zaciągnięty dług na kwotę 1 będzie spłacony po $n$ latach. Zdyskontowana wartość tej płatności jest równa $v n$ . Odsetki spłacane są na bieżąco, na początku każdego roku w wysokości $d$

Natomiast w przypadku płatności na koniec roku stosujemy oznaczenie $a_{\overline{n}|}$ i wartość obecną wyrażamy następująco

Po przekształceniu otrzymujemy:

Interpretacja tego wzoru jest taka sama jak zaprezentowana wyżej z tą tylko różnicą, że płatności odsetek wnoszone są na koniec roku w wysokości $d / v$ czyli $i$ .

Analogiczna do powyższych formuła dla rent ciągłych ma postać:

[edytuj] Model demograficzny

Punktem wyjścia do rozważań na temat ubezpieczeń na życie jest analiza trwania ludzkiego życia i momentu jego końca jako zjawiska o charakterze losowym. W niniejszym rozdziale omówiony zostaną podstawowe zagadnienia związane z modelem demograficznym.

W swej najprostszej wersji model ten zakłada, że śmierć danego osobnika następuje w losowym (czyli niemożliwym do dokładnego przewidzenia w sposób pewny) momencie a szanse zajścia lub nie takiego zdarzenia rozpatrujemy tylko i wyłącznie jako funkcję wieku osobnika. Uwzględnienie czynników pokoleniowych jest możliwe, ale wymagać będzie większej komplikacji modelu.

[edytuj] Zmienne losowe i inne oznaczenia

Obiektem naszych rozważań będzie osobnik w wieku $x$ i oznaczać go będziemy symbolem $(x)$ . Interesować nas będzie również jego wiek w chwili zgonu (czyli całkowita długość trwania jego życia) rozumiana jako zmienna losowa i oznaczana symbolem $X$ . Ponieważ $(x)$ jest obecnie w wieku $x$ , to pozostało przed nim jeszcze $X - x$ lat życia. Wprowadzamy więc zmienną losową $T (x)$ , zapisywaną czasem bez argumentu jako $T$ i definiujemy ją następująco:

Kolejnymi symbolami jakie wprowadzimy będą oznaczenia gęstości i dystrybuant dla rozważanych zmiennych losowych. Będą to odpowiednio $f$ i $F$ dla zmiennej $X$ oraz $g$ i $G$ dla zmiennej $T$ .

Wszystkie powyższe wartości nie muszą być liczbami całkowitymi. W praktyce dość często wiek jest wyrażany całkowitymi liczbami ukończonych lat życia. Również ubezpieczenia zawierane są często na konkretną liczbę lat. Całkowitą liczbę lat jakie $(x)$ przeżyje nim umrze oznaczymy przez $K$ .

Wszystkie powyższe oznaczenia zostały zebrane w tabeli:

ozn.	opis
$(x)$	osobnik w wieku $x$
$X$	wiek w chwili zgonu
$F (t)$	dystrybuanta zmiennej $X$
$f (t)$	gęstość zmiennej $X$
$T$	dalsze trwanie życia osoby $(x)$
$G (t)$	dystrybuanta zmiennej $T$
$g (t)$	gęstość zmiennej $T$
$K$	całkowita liczba przeżytych lat

[edytuj] Podstawowe prawdopodobieństwa występujące w modelu

Przyjąwszy powyższe oznaczenia możemy rozpocząć rozważania nad prawdopodobieństwem, że $(x)$ przeżyje lub nie zadany okres czasu $t$ . Prawdopodobieństwa te będą rzecz jasna funkcjami dwóch zmiennych - $x$ i $t$ . W notacji aktuarialnej są one oznaczane jako $t p x$ i $t q x$ . Umownie, gdy czas $t = 1$ to jest on w tym zapisie pomijany.

Wprowadzamy również funkcję $s (x)$ zwaną funkcją przeżycia. Definiuje się ją jako prawdopodobieństwo, że $(0)$ (czyli noworodek) dożyje wieku $x$

Poniższa tabela zwięźle ujmuje wprowadzone oznaczenia

oznaczenie	definicja	założenia
$F(x)\,$	$Pr(X\leq x)\,$	$x\geqslant0\,$
$s(x)\,$	$Pr(X>x)\,$	$x\geqslant0\,$
${}_{t}p_{x}\,$	$Pr(T(x)>t)\,$	$x,t\geqslant0\,$
${}_{t}q_{x}\,$	$Pr(T(x)\leq t)\,$	$x,t\geqslant0\,$
${}_{s\|t}q_{x}\,$	$Pr(s<T(x)<s+t)\,$	$x,s,t\geqslant0\,$
${}_{k\|}q_{x}\,$	$Pr(K(x)=k)\,$	$x\geqslant0,k\in\mathbb{N}\cup\{0\}\,$
${}_{k}p_{x}\,q_{x+k}\,$	$Pr(K(x)=k)\,$	$x\geqslant0,k\in\mathbb{N}\cup\{0\}\,$

[edytuj] Zależności

Każdy człowiek w danym okresie czasu może albo umrzeć albo nie. Nie istnieje trzecia możliwość a zatem prawdopodobieństwa $t p x$ i $t q x$ muszą dawać w sumie $1$

Można łatwo wykazać interpretując $t p x + s$ jako prawdopodobieństwo warunkowe przeżycia przez $x$ -latka $t + s$ lat pod warunkiem, że przeżyje on co najmniej $s$ lat ( $t p x + s = P r (T > s + t | T > s)$ ), że zachodzi równość

Podobnie można zinterpretować $s | t q x$

Kolejna warta zapamiętania zależność również łatwa do uzyskania w podobny sposób to:

[edytuj] Intensywność umieralności

Chcielibyśmy czasem mieć możliwość oceny prawdopodobieństwa zgonu nie w pewnym przedziale czasu ale lokalnie w danym momencie $t$ . Prawdopodobieństwo $x p x$ jest równe $0$ . Musimy więc rozważać niezerowe przedziały i dokonać przejścia granicznego czyli innymi słowy posłużyć się pojęciem pochodnej. Definiuje się więc wielkość zwaną intensywnością umieralności, oznaczaną $μ x$ i określoną następująco

Prawdopodobieństwo występujące w powyższym wzorze można wyrazić za pomocą funkcji przeżycia

Po podstawieniu otrzymujemy

Współczynnik umieralności można również wyrazić w terminach prawdopodobieństw $t p x$

[edytuj] Modele analityczne

Życie ludzkie jest procesem na który wpływ ma wiele czynników. Różne czynniki mają wpływ na śmiertelność w różnym wieku. W każdej populacji rozkład zmiennej $T$ jest nieco inny. W XVIII i XIX w. podejmowano jednak próby opisania śmiertelności w sposób analityczny. Dziś modele te mają już raczej charakter wyłącznie historyczny, a próby analitycznego opisania rozkładu długości trwania życia spotykają się ze sceptyczną oceną demografów.

W 1724 r. Abraham de Moivre przyjął założenie, że istnieje nieprzekraczalny wiek graniczny $ω$ . Założył również, że dalsze trwanie życia $(x)$ ma rozkład jednostajny na przedziale $(0,ω - x)$ . Natężenie wymierania w takim modelu wyraża się wzorem

O hipotetycznej populacji, w której umieralność spełnia powyższe równanie mówi się, że rządzi nią prawo umieralności de Moivre

W 1824 r. Benjamin Gompertz postawił hipotezę, że wiek graniczny nie istnieje a współczynnik umieralności jest funkcją wykładniczą.

W 1860 r. William Makeham uzupełnił formułę Gompertza o stały, niezależny od wieku człon $A$ .

Warto zauważyć, że w modelach Gompertza i Makehama gdy $c = 1$ to współczynnik umieralności byłby stały (niezależny od wieku). Oznaczałoby to, że człowiek niezależnie od wieku ma przed sobą takie same perspektywy odnośnie długości dalszego trwania życia. Innymi słowy w takiej populacji nikt się nie starzeje, długość życia ma rozkład wykładniczy, a umieralność można wtedy porównać do procesu rozpadu promieniotwórczego.

W 1939 r. szwedzki inżynier i matematyk Ernst Hjalmar Waloddi Weibull zaproponował użycie funkcji wielomianowej w miejsce wykładniczej

[edytuj] Tablice długości trwania życia

Podstawowe dane demograficzne niezbędne do kalkulacji aktuarialnych gromadzone są w formie tablic długości trwania życia. Tablice takie publikowane są w Polsce przez Główny Urząd Statystyczny^[1]. Mają one formę tabeli w której osobno dla mężczyzn a osobno dla kobiet znajdują się dane zebrane w kolumnach:

$x\,$	$l_{x}\,$	$q_{x}\,$	$d_{x}\,$	$L_{x}\,$	$T_{x}\,$	$\stackrel{\circ}{e}_{x}$

$x$ – wiek w latach,
$l x$ – średnia liczba dożywających wieku $x$ spośród początkowej liczby $l_{0}=100\,000$ noworodków,
$q x$ – jak wyjaśniono wcześniej jest to prawdopodobieństwo, że $(x)$ przeżyje co najwyżej kolejny rok,
$d x : = l x - l x + 1$ – średnia liczba zgonów w przedziale wieku od $x$ do $x + 1$
$L x$ – średnia ogólna liczba przeżytych lat pomiędzy wiekiem $x$ i $x + 1$ z początkowej kohorty $l_{0}=100\,000$ noworodków,
$T x$ – średnia ogólna liczba przeżytych lat powyżej wieku $x$ dla początkowej kohorty $l_{0}=100\,000$ noworodków,
$\stackrel{\circ}{e}_{x}$ – oczekiwana dalsza długość trwania życia dla $(x)$ .

Symbol $d x$ jest szczególnym przypadkiem symbolu $n d x$ definiowanego następująco:

Symbol $\stackrel{\circ}{e}_{x}$ definiuje się następująco:

Dla zmiennej dyskretnej $K (x)$ również definiuje się analogiczny symbol:

Ponadto można pokazać, że:

Ubezpieczyciele do swych kalkulacji korzystają z własnych tablic, które nie są ogólnie dostępne.

[edytuj] Prawdopodobieństwo zgonu dla okresów ułamkowych

Dane demograficzne zebrane w tablicach długości trwania życia mają charakter dyskretny. Dostarczają informację o konkretnych wartościach jedynie dla wartości całkowitych. Gdy chcemy uzyskać dane dla konkretnego momentu pomiędzy tymi wartościami musimy dokonać interpolacji. W podrozdziale niniejszym omówimy trzy podstawowe założenia dla interpolacji stosowanej w ubezpieczeniach na życie.

Nieco bardziej formalnie i korzystając z wprowadzonych oznaczeń ujmujemy to zagadnienie następująco. Znamy rozkład zmiennej $K$ i na jego podstawie chcemy interpolować rozkład zmiennej $T$ . Wprowadzamy oznaczenie $S$ :

 $S : = T - K .$

[edytuj] Jednostajny rozkład zgonów w ciągu roku (UDD)

Założenie to określane jest skrótem UDD (ang. uniform distribution of deaths). Już z samej nazwy widać, że przy założeniu tym $S$ ma rozkład jednostajny na przedziale jednego roku. Zakładać ponadto będziemy, że zmienne $K$ i $S$ są niezależne. Z jednostajności rozkładu zgonów w ciągu roku wynika liniowość prawdopodobieństwa $t q x$ względem $t$ w przedziale $(0,1)$ czyli

[edytuj] Stała intensywność umieralności

Zakładamy tu, że $μ x + t$ ma dla każdego $t\in(0,1)$ wartość stałą równą $\mu_{x+\frac{1}{2}}=-\ln p_{x}.$

Przy tym założeniu zmienne $K$ i $S$ nie są niezależne.

[edytuj] Założenie Balducciego

Założenie to określone jest wzorem:

Idea tego założenia polega na liniowej interpolacji odwrotności funkcji przeżycia:

Przy tym założeniu zmienne $K$ i $S$ nie są niezależne.

[edytuj] Podsumowanie

funkcja	UDD	$\mu=const\,$	Balducci
${}_{t}q_{x}\,$	$tq_{x}\,$	$1-e^{-\mu t}\,$	$\frac{tq_{x}}{1-(1-t)q_{x}}\,$
${}_{t}p_{x}\,$	$1-tq_{x}\,$	$e^{-\mu t}\,$	$\frac{p_{x}}{1-(1-t)q_{x}}\,$
${}_{y}q_{x+t}\,$	$\frac{yq_{x}}{1-tq_{x}}\,$	$1-e^{-\mu y}\,$	$\frac{yq_{x}}{1-(1-t)q_{x}}\,$
$\mu_{x+t}\,$	$\frac{q_{x}}{1-tq_{x}}\,$	$\mu\,$	$\frac{q_{x}}{1-(1-t)q_{x}}\,$
${}_{t}p_{x}\mu_{x+t}\,$	$q_{x}\,$	$e^{-\mu t}\mu\,$	$\frac{p_{x}q_{x}}{1-(1-t)q_{x}}\,$
$\stackrel{\circ}{e}_{x}\,$	$e_{x}+\frac{1}{2}\,$
$Var(T)\,$	$Var(K)+\frac{1}{12}\,$

[edytuj] Tablice specjalne

Tablice długości trwania życia są skonstruowane dla poszczególnych grup zróżnicowanych według różnych czynników. Najważniejszym czynnikiem branym pod uwagę przy zawarciu ubezpieczenia jest wiek początkowy $x$ . Ubezpieczenia jednak są oferowane często osobom cieszącym się dobrym zdrowiem. Często również przed przystąpieniem do ubezpieczenia wykonywane są badania medyczne. Sytuacja takiej osoby nie jest więc identyczna z sytuacją $x$ -latka, który wykupił ubezpieczenie kilka lat temu nawet jeśli inne czynniki są identyczne. Aby wziąć to pod uwagę konstruuje się tablice specjalne (selektywne, ang. select life tables). W tablicach takich prawdopodobieństwa śmierci są różne w zależności od wieku przystąpienia do ubezpieczenia. Wprowadza się zatem oznaczenie $q [x] + t$ jako prawdopodobieństwo, że osoba $(x + t)$ , która przystąpiła do ubezpieczenia w wieku $x$ umrze w ciągu najbliższego roku. Zachodzi przy tym nierówność

Po kilku latach (powiedzmy $r$ ) wiek w chwili przystąpienia przestaje mieć tak duże znaczenie i można używać zwykłych tablic. Zachodzi więc

[edytuj] Przypisy

↑ Tablice trwania życia

[edytuj] Podstawowe ubezpieczenia życiowe

Podobnie jak w przypadku teorii oprocentowania, rozpoczniemy od najprostszych ubezpieczeń w których kwota świadczenia jest równa $1$ . Znamy kwotę jaką otrzymamy. Tym więc o co będziemy pytać będzie wartość obecna tego świadczenia. Będziemy więc zastanawiać się nad tym ile trzeba zapłacić jednorazowo (bez uwzględnienia kosztów ubezpieczyciela) by uzyskać dane ubezpieczenie. Kwotę taką będziemy nazywać jednorazową składką netto (NSP – Net Single Premium) Wartość obecna netto ubezpieczeń na życie jest oznaczana literą $A$ z odpowiednimi indeksami określającymi typ ubezpieczenia.

Oznaczmy przez $Z$ wartość obecną wartością obecną netto (NPV – Net Present Value) świadczenia wypłacanego z tytułu danej polisy. Ustalając wartość obecną netto ubezpieczenia nie możemy posłużyć się wzorami deterministycznymi ponieważ są one uzależnione od czynnika losowego. By dokonać wyceny netto ubezpieczenia musimy posłużyć się wartością oczekiwaną zmiennej losowej $Z$ . Postępowanie takie jest uzasadnione wnioskami płynącymi z prawa wielkich liczb. Suma wielu realizacji zmiennej losowej $Z$ będzie wraz ze wzrostem ich liczby $n$ dążyć do $n\cdot E(Z)$ a zatem kwota potrzebna na wypłatę świadczeń dużej liczbie ubezpieczonych będzie w przybliżeniu równa wartości oczekiwanej takiej wypłaty przemnożonej przez liczbę wystawionych polis.

Ubezpieczenia na życie według momentu wypłaty świadczenia dzieli się na:

płatne na koniec roku śmierci
płatne w chwili śmierci
płatne na koniec podokresu roku śmierci (miesiąc, kwartał)

Ze względu na okres odpowiedzialności ubezpieczeniowej, ubezpieczenia można podzielić na:

ubezpieczenia na życie, bezterminowe
ubezpieczenia na życie, terminowe
ubezpieczenia na dożycie
ubezpieczenia na życie i dożycie
odroczone ubezpieczenia na życie, bezterminowe
odroczone ubezpieczenia na życie, terminowe

Oprócz ubezpieczeń na kwotę jednostkową rozważa się jeszcze ubezpieczenia:

rosnące (kwota świadczenia wzrasta o 1 co roku)
malejące (kwota świadczenia maleje o 1 co roku)

przy czym zmiana wysokości świadczenia może następować w sposób ciągły lub skokowy w okresach rocznych lub podokresach.

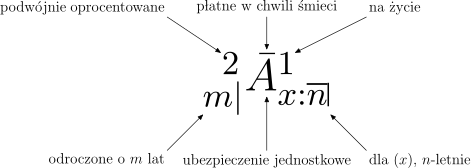
Powyższy rysunek ilustruje sposób odczytywania symboli aktuarialnych.

[edytuj] Ubezpieczenia płatne na koniec roku śmierci

Ozn.	$E(Z)\;$	$Var(Z)=E(Z^{2})-E^{2}(Z)\;$	$Z\;$
$A_{x}\;$	$\sum\limits_{k=0}^{\infty}v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$	${}^{2}A_{x}-A_{x}^{2}\;$	$v^{k+1}\quad\text{dla }k=0,1,\ldots\;$
$A_{x:\overline{n}\|}^{1}\;$	$\sum\limits_{k=0}^{n-1}v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$	${}^{2}A_{x:\overline{n}\|}^{1}-\left(A_{x:\overline{n}\|}^{1}\right)^{2}\;$	$\begin{cases} v^{k+1}&\text{dla }k=0,1,\ldots,n-1 \\ 0&\text{dla }k=n,n+1,n+2,\ldots \end{cases}\;$
$A_{x:\overline{n}\|}^{\;\;\;1}\;$	$v^{n}{}_{n}p_{x}\;$	${}^{2}A_{x:\overline{n}\|}^{\;\;\;1}-\left(A_{x:\overline{n}\|}^{\;\;\;1}\right)^{2}\;$	$\begin{cases} 0&\text{dla }k=0,1,\ldots,n-1 \\ v^{n}&\text{dla }k=n,n+1,n+2,\ldots \end{cases}\;$
$A_{x:\overline{n}\|}\;$	$A_{x:\overline{n}\|}^{1}+A_{x:\overline{n}\|}^{\;\;\;1}\;$	${}^{2}A_{x:\overline{n}\|}-\left(A_{x:\overline{n}\|}\right)^{2}\;$	$\begin{cases} v^{k+1}&\text{dla }k=0,1,\ldots,n-1 \\ v^{n}&\text{dla }k=n,n+1,n+2,\ldots \end{cases}\;$
${}_{m\|n}A_{x}\;$	$A_{x:\overline{n}\|}^{1}-A_{x:\overline{m}\|}^{1}\;$	${}^{\;\;\;2}_{m\|n}A_{x}-\left({}_{m\|n}A_{x}\right)^{2}\;$	$\begin{cases} 0&\text{dla }k=0,1,\ldots,m-1 \\ v^{k+1}&\text{dla }k=m,m+1,m+2,\ldots,m+n-1\\ 0&\text{dla }k=m+n,m+n+1,\ldots \end{cases}\;$
${}_{m\|}A_{x}\;$	$A_{x}-A_{x:\overline{m}\|}^{1}\;$	${}^{\;\;\;2}_{m\|}A_{x}-\left({}_{m\|}A_{x}\right)^{2}\;$	$\begin{cases} 0&\text{dla }k=0,1,\ldots,m-1 \\ v^{k+1}&\text{dla }k=m,m+1,m+2,\ldots\\ \end{cases}\;$
$(IA)_{x:\overline{n}\|}^{1}\;$	$\sum\limits_{k=0}^{n-1}(k+1)v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$		$\begin{cases} (k+1)v^{k+1}&\text{dla }k=0,1,\ldots,n-1 \\ 0&\text{dla }k=n,n+1,n+2,\ldots \end{cases}\;$
$(DA)_{x:\overline{n}\|}^{1}\;$	$\sum\limits_{k=0}^{n-1}(n-k)v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$		$\begin{cases} (n-k)v^{K+1}&\text{dla }k=0,1,\ldots,n-1 \\ 0&\text{dla }k=n,n+1,n+2,\ldots \end{cases}\;$
$(IA)_{x}\;$	$\sum\limits_{k=0}^{\infty}(k+1)v^{k+1}{}_{k}p_{x}\,q_{x+k}\;$		$(k+1)v^{k+1}\quad\text{dla }k=0,1,\ldots\;$

[edytuj] Ubezpieczenia płatne w chwili śmierci

Ozn.	$E(Z)\;$	$Var(Z)=E(Z^{2})-E^{2}(Z)\;$	$Z\;$
$\bar{A}_{x}\;$	$\int\limits_{0}^{\infty}v^{t}{}_{t}p_{x}\mu_{x+t}dt\;$	${}^{2}\bar{A}_{x}-\bar{A}_{x}^{2}\;$	$v^{t}\quad\text{dla }t\in(0,+\infty)\;$
$\bar{A}_{x:\overline{n}\|}^{1}\;$	$\int\limits_{0}^{n}v^{t}{}_{t}p_{x}\mu_{x+t}dt\;$	${}^{2}\bar{A}_{x:\overline{n}\|}^{1}-\left(\bar{A}_{x:\overline{n}\|}^{1}\right)^{2}\;$	$\begin{cases} v^{t}&\text{dla }t\in(0,n] \\ 0&\text{dla }t\in(n,+\infty) \end{cases}\;$
$A_{x:\overline{n}\|}^{\;\;\;1}\;$	$v^{n}{}_{n}p_{x}\;$	${}^{2}A_{x:\overline{n}\|}^{\;\;\;1}-\left(A_{x:\overline{n}\|}^{\;\;\;1}\right)^{2}\;$	$\begin{cases} 0&\text{dla }t\in(0,n]\\ v^{n}&\text{dla }t\in(n,+\infty) \end{cases}\;$
$\bar{A}_{x:\overline{n}\|}\;$	$\bar{A}_{x:\overline{n}\|}^{1}+A_{x:\overline{n}\|}^{\;\;\;1}\;$	${}^{2}\bar{A}_{x:\overline{n}\|}-\left(\bar{A}_{x:\overline{n}\|}\right)^{2}\;$	$\begin{cases} v^{t}&\text{dla }t\in(0,n]\\ v^{n}&\text{dla }t\in(n,+\infty) \end{cases}\;$
${}_{m\|n}\bar{A}_{x}\;$		${}^{\;\;\;2}_{m\|n}A_{x}-\left({}_{m\|n}A_{x}\right)^{2}\;$	$\begin{cases} 0&\text{dla }t\in(0,n] \\ v^{n}&\text{dla }t\in(n,n+m]\\ 0&\text{dla }t\in(m+n,+\infty) \end{cases}\;$
$(\bar{I}\bar{A})_{x:\overline{n}\|}^{1}\;$	$\int\limits_{0}^{n}tv^{t}{}_{t}\,p_{x}\mu_{x+t}dt\;$		$\begin{cases} [t+1]v^{t}&\text{dla }t\in(0,n]\\ 0&\text{dla }t\in(n,+\infty) \end{cases}\;$
$(\bar{D}\bar{A})_{x:\overline{n}\|}^{1}\;$	$\int\limits_{0}^{n}(n-t)v^{t}{}_{t}\,p_{x}\mu_{x+t}dt\;$		$\begin{cases} (n-[t])v^{t}&\text{dla }t\in(0,n] \\ 0&\text{dla }t\in(n,+\infty) \end{cases}\;$
$(\bar{I}\bar{A})_{x}\;$	$\int\limits_{0}^{\infty}tv^{t}{}_{t}\,p_{x}\mu_{x+t}dt\;$		$tv^{t}\quad\text{dla }t>0\;$

[edytuj] Zależności

Wzorów zaprezentowanych poniżej nie będziemy dowodzić. Ograniczymy się jedynie do krótkich interpretacji ułatwiających zapamiętanie.

Interpretacja: Ubezpieczenie na życie i dożycie jest sumą ubezpieczenia na życie i ubezpieczenia na dożycie.

Interpretacja: Ubezpieczony $(x)$ może umrzeć w ciągu najbliższego roku (z prawdopodobieństwem $q x$ ) i otrzymać świadczenie w wysokości $1$ , lub przeżyć najbliższy rok (z prawdopodobieństwem $p x$ ) i być ubezpieczonym $x + 1$ -latkiem z ubezpieczeniem o wartości $A x + 1$ . Będzie to za rok więc dyskontujemy czynnikiem dyskontującym $v$ .

Interpretacja: Jest to uogólnienie zależności opisanej powyżej. (Pamiętajmy, że $A_{x:\overline{n}|}^{\;\;\;1}=v^{n}{}_{n}p_{x}$ jest czynnikiem dyskontującym w sensie aktuarialnym tj. z uwzględnieniem prawdopodobieństwa przeżycia.)

Interpretacja: Ubezpieczenie o rosnącej kwocie świadczenia zawiera w sobie zwykłe ubezpieczenie na życie. Ponadto po roku dodatkowo pojawia się ubezpieczenie z kwotą rosnącą startującą od jedynki.

Interpretacja: Sumy kwot wypłat z tytułu ubezpieczenia z świadczeniem malejącym i rosnącym są w każdym roku jednakowe i równe $n + 1$ .

Przy założeniu UDD prawdziwe są zależności:

Dla ubezpieczeń na życie i dożycie analogiczna zależność nie zachodzi

[edytuj] Funkcje komutacyjne dla podstawowych ubezpieczeń

W dzisiejszych czasach przechowywanie dużej ilości danych i wykonywanie na nich obliczeń nie stanowi kłopotu za sprawą komputerów. Dawniej jednak istotne znaczenie miało aby dane niezbędne do skalkulowania składki dały się wydrukować na sensownej liczbie stron a sama kalkulacja nie nastręczała zbyt dużych trudności rachunkowych. Nie można więc było tworzyć tablicy zawierającej dane dla każdego wieku i każdego okresu ubezpieczenia. Wymyślono więc funkcje komutacyjne. Mają one obecnie znaczenie jedynie w dydaktyce matematyki ubezpieczeniowej.

Przyjmuje się następujące oznaczenia

Wtedy wartości aktuarialne poszczególnych ubezpieczeń oblicza się następująco

[edytuj] Renty życiowe (Life annuities)

Renty są ciągami płatności. W matematyce ubezpieczeniowej również i one są uzależnione długością trwania życia. Za pomocą rent opisywać będziemy przepływy finansowe zarówno od ubezpieczonego do ubezpieczyciela (jak to ma miejsce w przypadku składek) jak i od ubezpieczyciela do ubezpieczonego (jak to ma miejsce w przypadku świadczeń emerytalnych).

Podobnie jak w przypadku wartości obecnej ubezpieczeń mamy tu do czynienia z podziałem rent wg różnych czynników.

Wg długości trwania renty dzielimy na:

terminowe,
bezterminowe,
terminowe odroczone,
bezterminowe odroczone.

Wg czasu dokonywania płatności renty dzielimy na płatne:

na początku roku lub jego podokresu okresu,
na koniec roku lub jego podokresu okresu,
w sposób ciągły.

[edytuj] Renty dyskretne

symbol	wartość	relacja	nazwa
$\ddot{a}_{x} \,$	$\sum_{k=0}^{\infty}v^{k}{}_{k}p_{x}\,$	$1=d\ddot{a}_{x}+A_{x}\,$	bezterminowa, płatna na początku każdego roku
$a_{x} \,$	$\sum_{k=1}^{\infty}v^{k}{}_{k}p_{x}\,$		bezterminowa, płatna na końcu każdego roku
$\ddot{a}_{x:\overline{n}\|} \,$	$\sum_{k=0}^{n-1}v^{k}{}_{k}p_{x}\,$	$1=d\ddot{a}_{x:\overline{n}\|}+A_{x:\overline{n}\|}\,$	$n$ -letnia, płatna na początku każdego roku
$a_{x:\overline{n}\|} \,$	$\sum_{k=1}^{n}v^{k}{}_{k}p_{x}\,$		$n$ -letnia, płatna na końcu każdego roku
${}_{n\|}\ddot{a}_{x} \,$	$\sum_{k=n}^{\infty}v^{k}{}_{k}p_{x}\,$		bezterminowa, płatna na początku każdego roku, odroczona o $n$ lat
${}_{n\|}a_{x} \,$	$\sum_{k=n+1}^{\infty}v^{k}{}_{k}p_{x}\,$		bezterminowa, płatna na końcu każdego roku, odroczona o $n$ lat

W powyższej tabeli prócz wzorów definicyjnych podano również relacje jakie zachodzą pomiędzy rentami a wartościami obecnymi ubezpieczeń na życie. Sens tych relacji można wyjaśnić na następującym przykładzie:

Interpretacja tego wzoru może być następująca. Zaciągnięto dług na kwotę $1$ . Dłużnik spłaca same odsetki na początku każdego roku (w wysokości $d$ ). Ponieważ dłużnik może umrzeć przed uregulowaniem długu, wykupił ubezpieczenie gwarantujące uregulowanie pozostałej do spłaty należności. Następuje to na koniec roku śmierci ubezpieczonego.

[edytuj] Renty ciągłe

symbol	wartość	relacja
$\bar{a}_{x}\,$	$\int_{0}^{\infty}v^{t}{}_{t}p_{x}dt\,$	$1=\delta\bar{a}_{x}+\bar{A}_{x}\,$
$\bar{a}_{x:\overline{n}\|}\,$	$\int_{0}^{n}v^{t}{}_{t}p_{x}dt\,$	$1=\delta\bar{a}_{x:\overline{n}\|}+\bar{A}_{x:\overline{n}\|}\,$
${}_{n\|}\bar{a}_{x}\,$	$\int_{n}^{\infty}v^{t}{}_{t}p_{x}dt\,$
${}_{m\|n}\bar{a}_{x}\,$	$\int_{m}^{m+n}\!\!v^{t}{}_{t}p_{x}dt\,$

[edytuj] Renty płatne częściej niż raz w roku

gdzie

W większości wypadków (dla niewielkiego $δ$ ) można się posłużyć praktycznym przybliżeniem wynikającym z rozwinięcia powyższych wzorów w szereg Taylora:

[edytuj] Funkcje komutacyjne dla rent

[edytuj] Składki netto (Net premiums)

Umowa ubezpieczeniowa jest umową dwustronną pomiędzy ubezpieczycielem a ubezpieczonym. Określa ona jakie obowiązki z jakich wywiązać musi się każda ze stron. Z jednej więc strony określone są świadczenia wypłacane przez ubezpieczyciela, a z drugiej składki czyli płatności jakie odprowadza ubezpieczycielowi ubezpieczony. Zarówno świadczenia jak i składki mogą mieć charakter jednorazowych płatności lub ich ciągu o stałej lub zmiennej wartości. W sytuacji kalkulacji netto świadczenia i składki są sobie w sensie aktuarialnym równoważne. Oznacza to, że wartości oczekiwane przepływów finansowych będą równe.

Wprowadzimy teraz pojęcie straty ubezpieczyciela. Wielkość tą jest zmienną losową oznaczaną literą $L$ (ang. total loss) i będącą różnicą między wypłaconymi świadczeniami i zebranymi składkami dla danego ubezpieczonego. Składki będą ustalone na poziomie netto jeśli spełniona będzie równość

Literą używaną do oznaczania składek netto jest litera $P$ od angielskiego net premium.

[edytuj] Przykład

Obliczenie składki netto zobrazujemy na przykładzie bezterminowej polisy na życie, z wypłatą świadczenia na koniec roku zgonu. Przyjmijmy, że opłacane ono będzie stałą składką $P x$ na początku każdego roku. Wtedy stratę ubezpieczyciela można wyrazić za pomocą całkowitej liczby $K$ pozostałych lat życia jako różnicę zdyskontowanej wypłaty świadczenia oraz wartości obecnej renty przemnożonej przez wartość składki

Wiemy, że musi zachodzić $E (L) = 0$ zatem

[edytuj] Funkcje komutacyjne w kalkulacji składek netto

[edytuj] Rezerwy składek netto (Net premium reserves)

Jak dotąd opisaliśmy za pomocą aparatu matematycznego zawarcie ubezpieczenia, napływanie składek i wypłacanie świadczeń. Wydawać by się mogło, że można na tym poprzestać. W tym rozdziale przekonamy się, że tak nie jest. Ubezpieczyciel powinien w każdym momencie znać wartość rezerw składek netto czyli kwoty jaką dysponuje na pokrycie nieuchronnie zbliżających się świadczeń jakie będzie musiał wypłacić z tytułu jego ubezpieczenia. Wiedza ta potrzebna jest nie tylko po to by zapanować nad zarządzanym kapitałem. Jest ona niezbędna w sytuacji konwersji polisy czyli zmiany jej warunków z uwzględnieniem dotychczas wniesionych składek. Przykładowo w sytuacji gdy ubezpieczony przez wiele lat regularnie wnosił składki, a w pewnym momencie nie jest już w stanie tego robić, to często taka polisa przekształcana jest w polisę bezskładkową o odpowiednio niższej kwocie świadczenia.

Dodatkowo jak się przekonamy rezerwy netto to nie tylko suma składek wniesionych przez ubezpieczonego. Produkty oferowane przez ubezpieczycieli zawierają w sobie zawsze element ryzyka^[1]. Jest ono związane m.in. z możliwością zgonu poza okresem objętym ubezpieczeniem, długością trwania wypłaty świadczenia w postaci renty lub długością trwania okresu opłacania składek. Istotnym czynnikiem kształtujących wysokość rezerwy jest właśnie to ryzyko.

[edytuj] Definicja i podstawowe wzory

W poprzednim rozdziale wprowadziliśmy pojęcie straty ubezpieczyciela $L$ . Tu uogólnimy nieco to pojęcie wprowadzając pojęcie straty $k L$ ubezpieczyciela po $k$ latach od wystawienia polisy. Tę zmienną losową definiuje się tak samo jak zwykłą stratę (czyli stratę w chwili zawarcia ubezpieczenia) z tą tylko różnicą, że przyjmuje się warunek, że ubezpieczony przeżyje $k$ lat od chwili zawarcia ubezpieczenia.

Rezerwą nazywać będziemy wartość oczekiwaną tej straty.

Ponieważ $0 L = L$ więc zachodzi oczywiście $0 V x = E (L) = 0.$

[edytuj] Przykład

[edytuj] Wzory

Poniżej przedstawiamy podstawowe wzory służące do kalkulacji rezerw:

[edytuj] Funkcje komutacyjne w kalkulacji rezerw

[edytuj] Przypisy

↑ Prawo zabrania firmom ubezpieczeniowym oferowania produktów nie będących ubezpieczeniami, a więc nie mających charakteru ochrony na wypadek ryzyka wystąpienia skutków zdarzeń losowych. Porównaj Artykuł 3. ustępy 1. i 2. ustawy z dnia 22 maja 2003 r. o działalności ubezpieczeniowej Dz.U. 2003 nr 124 poz. 1151 (http://isip.sejm.gov.pl/servlet/Search?todo=open&id=WDU20031241151).

[edytuj] Składki i rezerwy brutto

Matematyka ubezpieczeń życiowych/Składki i rezerwy brutto

[edytuj] Wielorakie szkodowości (Multiple decrements)

Inwalidztwo, utrata możliwości zarobkowania, choroba wymagająca długotrwałego kosztownego leczenia a także inne porównywalne zdarzenia losowe mogą być czasem podobnie dotkliwe dla rodziny ubezpieczonego jak jego śmierć. Zakłady ubezpieczeń na życie oferują obecnie ubezpieczenia uwzględniające również i takie zdarzenia losowe^[1]. Aby móc zajmować się takimi ubezpieczeniami niezbędny jest matematyczny model uwzględniający wystąpienie jednego z kilku zdarzeń będących podstawą wypłaty świadczenia w odpowiedniej dla danej szkody wysokości. Jest to model szkodowości wielorakiej (ang. multiple decrement model).

[edytuj] Przypisy

↑ Należy pamiętać, że jedna firma ubezpieczeniowa nie może oferować jednocześnie ubezpieczeń na życie (Dział I) i ubezpieczeń majątkowych (Dział II) jednak załącznik do ustawy wyliczając ryzyka z poszczególnych działów precyzuje, że do ubezpieczeń działu I zalicza się również ubezpieczenia wypadkowe i chorobowe, jako uzupełnienie pozostałych ubezpieczeń z tego działu. (http://isip.sejm.gov.pl/servlet/Search?todo=open&id=WDU20031241151)

[edytuj] Ubezpieczenia grupowe

Matematyka ubezpieczeń życiowych/Ubezpieczenia grupowe

[edytuj] Fundusze emerytalne

Matematyka ubezpieczeń życiowych/Fundusze emerytalne

[edytuj] Literatura

Bowers N.L.J., Gerber H.U., Hickman J.C., Jones D.A., Nesbit C.J.: Actuarial Mathematics. Itasca: The Society of Actuaries, 1986. ISBN 0-938959-10-7.
Gerber H.U: Life Insurance Mathematics, Springer-Verlag, Berlin, Heidelberg, New York 1995. ISBN 0-387-52944-6.
Skałba M.: Ubezpieczenia na życie, Wydawnictwa Naukowo-Techniczne, Warszawa 1999. ISBN 83-204-2460-7.

[edytuj] WWW

[edytuj] Powiązane tematycznie hasła Wikipedii

[edytuj] Egzaminy aktuarialne w sieci

[edytuj] Strony różne

Tablice trwania życia
[1][2] – Rozporządzenie Ministra Finansów z dnia 20 listopada 2003 r. w sprawie zakresu obowiązujących tematów egzaminów aktuarialnych oraz trybu przeprowadzania tych egzaminów (Dz. U. z dnia 12 grudnia 2003 r.)
[3] – artykuł na temat notacji aktuarialnej

[0] Tablice trwania życia

[1] Prawo zabrania firmom ubezpieczeniowym oferowania produktów nie będących ubezpieczeniami, a więc nie mających charakteru ochrony na wypadek ryzyka wystąpienia skutków zdarzeń losowych. Porównaj Artykuł 3. ustępy 1. i 2. ustawy z dnia 22 maja 2003 r. o działalności ubezpieczeniowej Dz.U. 2003 nr 124 poz. 1151 (http://isip.sejm.gov.pl/servlet/Search?todo=open&id=WDU20031241151).

[2] Należy pamiętać, że jedna firma ubezpieczeniowa nie może oferować jednocześnie ubezpieczeń na życie (Dział I) i ubezpieczeń majątkowych (Dział II) jednak załącznik do ustawy wyliczając ryzyka z poszczególnych działów precyzuje, że do ubezpieczeń działu I zalicza się również ubezpieczenia wypadkowe i chorobowe, jako uzupełnienie pozostałych ubezpieczeń z tego działu. (http://isip.sejm.gov.pl/servlet/Search?todo=open&id=WDU20031241151)

[1]

[1]

[1]

Matematyka ubezpieczeń życiowych/Wersja do druku

Z Wikibooks, biblioteki wolnych podręczników.

Spis treści

[edytuj] Wprowadzenie

[edytuj] Elementy teorii oprocentowania

[edytuj] Akumulacja i dyskontowanie

[edytuj] Przypadek dyskretny

[edytuj] Przypadek ciągły

[edytuj] Podsumowanie

[edytuj] Renty

[edytuj] Model demograficzny

[edytuj] Zmienne losowe i inne oznaczenia

[edytuj] Podstawowe prawdopodobieństwa występujące w modelu

[edytuj] Zależności

[edytuj] Intensywność umieralności

[edytuj] Modele analityczne

[edytuj] Tablice długości trwania życia

[edytuj] Prawdopodobieństwo zgonu dla okresów ułamkowych

[edytuj] Jednostajny rozkład zgonów w ciągu roku (UDD)

[edytuj] Stała intensywność umieralności

[edytuj] Założenie Balducciego

[edytuj] Podsumowanie

[edytuj] Tablice specjalne

[edytuj] Przypisy

[edytuj] Podstawowe ubezpieczenia życiowe

[edytuj] Ubezpieczenia płatne na koniec roku śmierci

[edytuj] Ubezpieczenia płatne w chwili śmierci

[edytuj] Zależności

[edytuj] Funkcje komutacyjne dla podstawowych ubezpieczeń

[edytuj] Renty życiowe (Life annuities)

[edytuj] Renty dyskretne

[edytuj] Renty ciągłe

[edytuj] Renty płatne częściej niż raz w roku

[edytuj] Funkcje komutacyjne dla rent

[edytuj] Składki netto (Net premiums)

[edytuj] Przykład

[edytuj] Funkcje komutacyjne w kalkulacji składek netto

[edytuj] Rezerwy składek netto (Net premium reserves)

[edytuj] Definicja i podstawowe wzory

[edytuj] Przykład

[edytuj] Wzory

[edytuj] Funkcje komutacyjne w kalkulacji rezerw

[edytuj] Przypisy

[edytuj] Składki i rezerwy brutto

[edytuj] Wielorakie szkodowości (Multiple decrements)

[edytuj] Przypisy

[edytuj] Ubezpieczenia grupowe

[edytuj] Fundusze emerytalne

[edytuj] Literatura

[edytuj] Literatura

[edytuj] WWW

[edytuj] Powiązane tematycznie hasła Wikipedii

[edytuj] Egzaminy aktuarialne w sieci

[edytuj] Strony różne

Widok

Osobiste

Nawigacja

Drukuj lub eksportuj

Szukaj

Narzędzia