Ogólna teoria względności/Współrzędne cylindryczne a tunel Einsteina-Rosena

Ogólna teoria względności

Współrzędne cylindryczne a tunel Einsteina-Rosena

Licencja
Autor: Mirosław Makowiecki Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność.

Wykaz modułów w książce
1Wprowadzenie do ogólnej teorii względności 2Nadmiarowe równania elementarne teorii grawitacji Einsteina z siłami niegrawitacyjnymi 3Tensor gęstości energii-pędu 4Właściwości skalaru tensora metrycznego 5Zasada wariacyjna w ogólnej teorii względności 6Zasada wariacyjna a grawitacja i pole elektromagnetyczne 7Słabe pola grawitacyjne 8Fizyka w słabozakrzywionych czasoprzestrzeniach 9Promieniowanie grawitacyjne 10Statyczne rozwiązanie Schwarzschilda w kulistosymetrycznym polu grawitacyjnym 11Ruch cząstki próbnej wokół masy statycznie sferycznej-rozwiązanie ogólne 12Geometria statycznych czasoprzestrzeni Schwarzschilda, a czarne dziury 13Współrzędne Kruskala-Szekeresa 14Współrzędne Eddingtona-Finkelsteina 15Współrzędne cylindryczne a tunel Einsteina-Rosena

Spis treści
1Współrzędne Einsteina-Rosena 2Interpretacja współrzędnych Einsteina-Rosena

Poprzedni rozdział: Współrzędne Eddingtona-Finkelsteina.

Podręcznik: Ogólna teoria względności.

Za pomocą współrzędnych Einsteina-Rossena dowiemy, że istnieją dwa światy, które złączają się przy r=r_g, tzn. świat 1 ze światem 2.

Współrzędne Einsteina-Rosena

Obierzmy metrykę Schwarzschilda i zakładajmy, że dt=0, a także $\phi ={{\pi } \over {2}}\;$ , wtedy interwał czasoprzestrzenny przy tych założeniach przyjmując współrzędne cylindryczne przyjmuje postać:

ds^{2}=-dl^{2}=-{{dr^{2}} \over {1-{{r_{g}} \over {r}}}}-r^{2}d\theta ^{2}\;

(15.1)

Naszym celem przy odpowiednio dobranych współrzędnych dojść do geometrii Schwarzschilda we współrzędnych cylindrycznych. We współrzędnych cylindrycznych dl², różniczka długości między dwoma infinitezymalnie bliskimi punktami jest napisana wedle:

dl^{2}=d\rho ^{2}+\rho ^{2}d\alpha ^{2}+dz^{2}\;

(15.2)

A teraz weźmy nowe zmienne przy pomocy których można zapisać odległość pomiędzy punktami odległymi od siebie nieskończenie blisko (15.2) zdefiniowanej przy pomocy promienia radialnego r i kąta θ i z, a także przy pomocy promienia Schwarzschilda r_g:

\rho =r\;

(15.3)

\alpha =\theta \;

(15.4)

z=\pm 2{\sqrt {r_{g}(r-r_{g})}}\;

(15.5)

Następnym krokiem jest policzenie różniczki zupełnej z wielkości "z" zdefiniowanej w punkcie (15.5), którą wyrazimy przy pomocy różniczki promienia radialnego r:

dz=\pm 2{{r_{g}} \over {2{\sqrt {r_{g}(r-r_{g})}}}}dr=\pm {{r_{g}} \over {\sqrt {r_{g}(r-r_{g})}}}dr\;

(15.6)

Po podniesieniu do kwadratu różniczki współrzędnej zetowej zdefiniowanej według (15.6) przy pomocy promienia radialnego r mamy:

dz^{2}={{r_{g}^{2}} \over {r_{g}(r-r_{g})}}dr^{2}\Rightarrow dz^{2}={{r_{g}} \over {r-r_{g}}}dr^{2}\;

(15.7)

Następnie policzmy różniczkę długości dl² zdefiniowanej w punkcie (15.2) przy pomocy kwadratu różniczki współrzędnej zetowej (15.7):

dl^{2}=d\rho ^{2}+\rho ^{2}d\alpha ^{2}+dz^{2}=dr^{2}+r^{2}d\theta ^{2}+{{r_{g}} \over {r-r_{g}}}dr^{2}=r^{2}d\theta ^{2}+dr^{2}\left[1+{{r_{g}} \over {r-r_{g}}}\right]=\;

=r^{2}d\theta ^{2}+dr^{2}\left[{{r-r_{g}+r_{g}} \over {r-r_{g}}}\right]=r^{2}d\theta ^{2}+dr^{2}{{r} \over {r-r_{g}}}={{dr^{2}} \over {1-{{r_{g}} \over {r}}}}+r^{2}d\theta ^{2}\;

(15.8)

Na podstawie definicji kwadratu różniczki interwału czasoprzestrzennego (15.1) i z definicji kwadratu infitezymalnej długości między dwoma zdarzeniami:

ds^{2}=-dl^{2}=-{{dr^{2}} \over {1-{{r_{g}} \over {r}}}}-r^{2}d\theta ^{2}\;

(15.9)

czyli otrzymujemy geometrię statystyczno cylindryczną Schwarzchilda dla dt=0 na podstawie definicji kwadratu infinitezymalnej zmiany interwału czasoprzestrzennego.

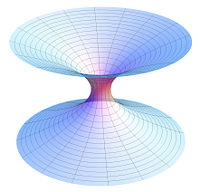
Interpretacja współrzędnych Einsteina-Rosena

W geometrii Einsteina-Rosena otrzymujemy dwa rozwiązania jedno dla z<0, a drugie dla z>0. Te oba światy są złączone dla r=r_g. W każdym bądź razie przez czarną dziurę przechodzi specyficzna gardziel zwaną tunelem Einsteina-Rosena. Można udowodnić, że analiza w geometrii Schwarzschilda nie pozwala na podróż, ze świata 1 do świata 2 w statyczno-sferycznej rozważanej geometrii.