Metody matematyczne fizyki/Grupy i ich reprezentacje
Licencja
|
|---|
|
Autor: Mirosław Makowiecki
Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność. |
Podręcznik: Metody matematyczne fizyki.
W fizyce z reguły każdy układ ma pewne wartości symetrii, które określamy po dokonaniu tejże symetrii układ pozostaje bez zmian. Wpływem działania grup symetrii na pewne układy zajmuje się tutaj dziedzina matematyki zwaną teorią grup i ich reprezentacji.
Warunki jakie musi spełniać para (G,⋅), by być grupą
[edytuj]Wybierzmy sobie zbiór G, w którym istnieje działanie, które w wyniku działania dwóch elementów tychże elementów należącej do tego zbioru powstaje element należącej do tej naszej grupy G.
- Dla każdych elementów
istnieje trzeci element
, które takie działanie dwóch elementów, których w wyniku powstaje trzeci element, określamy:

- W zbiorze G istnieje pewien element neutralny, które w wyniku pomnożenie przez dany element należącej do zbioru G lewostronnie czy prawostronnie powstaje ten sam element, co określamy:


- Dla każdego elementu a należącego do zbioru G istnieje element odwrotny a-1, który przy znajomości elementu neutralnego w zbiorze G określamy wedle:

- Działanie określone w zbiorze G dla grupy jest działaniem łącznym, co jest określane:

Grupy permutacji
[edytuj]Jest to grupa przekształceń skończonych, który w wyniku działania na l elementów otrzymujemy spermutowany wynik, który w zależności od argumentów wrzuconych do funkcji, różni się kolejnością elementów, lub w szczególności może nie być zmiany kolejności, co mamy do czynienia z permutacją tożsamościową. Określmy permutacja P określoną wedle wzoru na zbiorze n-elementowym należącej do zbioru X, co określamy schematem:

Odwzorowanie (16.6) jest działaniem wzajemnie jednoznacznym, zatem istnieje też operacja odwrotna do P. Działaniem grupowym dwóch permutacji określamy przez:

Elementem jednostkowym nazywamy permutacją identycznościową, która wyniku operacji (16.6) nie zmienia kolejności wyrazów. Liczba elementów permutacji skończonej jest równa liczbie n!
Grupa obrotów w przestrzeni trójwymiarowej
[edytuj]Załóżmy, że mamy oś obrotu wyznaczony przez jednostkowy wektor 

Inny sposobem obrotu naszego układu współrzędnych jest podanie trzech współrzędnych (θ,φ,ψ), które tworzą grupę obrotów określanych jako C(θ,φ,ψ). Popatrzmy na wzory (4.11), (4.12) i (4.13), a później oznaczmy je po kolei C3(φ), C1(θ), C3(ψ).

Jeśli zatem po pewnych omówieniach wstawimy za obroty występujące w punkcie (16.9) odpowiednie macierze, to otrzymamy macierz określoną przez wzór (4.15).
Translacje, inwersje i odbicia
[edytuj]Translacją jest to operacja polegająca na sztywnym przesunięciu całej przestrzeni o wektor 

Inwersją względem danego punktu nazywamy takie przekształcenie płaszczyzny, w której następuje zmiana znaku naszego wektora 

Aby otrzymać macierz inwersji, który działa na wektor 

Odbiciem względem płaszczyzny prostopadłej do wektora 



Definicje grupy cyklicznych, a także definicje podgrup i klas
[edytuj]- Grupa cykliczna jest to grupa, której elementy są potęgami pierwszego elementu nieneutralnego wchodzącej w skład grupy, to zbiór, który jest grupą, określamy:

Przykładem grupy obrotów cyklicznych jest grupa obrotów wokół ustalonej osi o kąty będącego wielokrotnością liczby 2π/n.
- Podgrupą nazywamy taki podzbiór H grupy G, którego działania dla poszczególnych elementów tejże grupy nie wychodzą poza granice tejże podgrupy.
- Klasa jest to zbiór K elementów danej grupy, który powstaje z jednego elementu b∈G, jest to zbiór określony;

Grupy symetrii na podstawie molekuły wody
[edytuj]Tutaj zbudujemy pewne działania na grupach symetrii dotyczącej molekuły wody (tlenku wodoru). Struktura przestrzenna cząsteczki wody jest pokazana na rysunku z prawej strony tego rozdziału. Grupy symetrii opisywanej tutaj cząsteczki wody przestawiamy wedle opisów:
- e - przekształcenie, które działa w sposób neutralny na dany obiekt i w rezultacie otrzymujemy ten sam obiekt wyjściowy do wejściowego, czyli jest to przekształcenie identycznościowe.
- C2 - jest to przekształcenie, która obraca dany obiekt o 180o względem osi pionowej.
- σ1 - jest to przekształcenie, które powoduje odbicie względem płaszczyzny prostopadłej do płaszczyzny rysunku.
- σ2 - jest to przekształcenie powodujące odbicie rysunku względem płaszczyzny w której jest zapisany ten rysunek.
Napiszemy w tabeli elementy działające na symetriach e, C2, σ1, σ2, ale działań przeprowadzonych w tabelce nie będziemy udowadniać.
G
|
e
|
C2
|
σ1
|
σ2
|
||
| e | e | C2 | σ1 | σ2 | ||
| C2 | C2 | e | σ2 | σ1 | ||
| σ1 | σ1 | σ2 | e | σ1 | ||
| σ2 | σ2 | σ1 | C2 | e |
Podziały grup na klasy
[edytuj]Każda grupę można podzielić na podzbiory, których zbiory nie pokrywają się ze sobą i działania obsługujące taką grupę nie wychodzą poza zakres tej naszej struktury, którą jest podgrupa. Wybierzmy teraz klasy (opisuje je schemat (16.17)) generowane przez dwa różne elementy a i b, wtedy jeśli te dwie klasy mają wspólne elementy, to powinno zachodzić na pewno 


W naszym rozważaniach w przypadku grupy (16.18) licząc jej elementy odwrotne, co piszemy:



Można udowodnić, że grupa G (16.18) dzieli się na trzy rozłączne klasy, których to klasy piszemy wedle przestawień:



Reprezentacji struktur, które są grupami
[edytuj]Własności opisywanych symetrii mają swój swoisty sposób, które są zapisywane w przestrzeni położeń R3 lub pośrednio określone na funkcjach w tej przestrzeni, operacje te zwykle przedstawiamy w macierzowej postaci i nazywać je będziemy reprezentacjami. Reprezentacją D grupy G jest to zbiór obiektów, które są macierzami kwadratowymi, które są homomorficzne z rozważaną grupą i spełniające podobne własności jak i rozważana grupa. Zgodnie z naszym postulatem możemy powiedzieć:



Warunki (16.25), (16.26) i (16.27) sugerują, że reprezentacje też są grupami.
Grupa symetrii wody
[edytuj]Symetrię molekuły wody już rozważaliśmy w rozdziale Grupy symetrii na podstawie molekuły wody, tylko tutaj podamy je w macierzowej wersji w rachunku reprezentacji, które są elementami odbicia, w takim razie ich odpowiednikami są macierze:


Grupa symetrii amoniaku
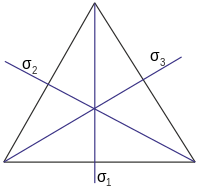
[edytuj]Symetrie cząsteczki amoniaku sprowadzają się do symetrii przekształceń trójkąta równobocznego. Ograniczmy się teraz do płaszczyzny, czyli do dwuwymiarowego układu współrzędnych, a środek umieszczać będziemy w środku geometrycznym trójkąta. Przekształceniami rządzącymi naszym trójkątem równobocznym są to transformacje typu C3ν, czyli są to transformacje, których omawiana grupa zawiera elementy zapisanej w punkcie (16.18), zatem w rachunku reprezentacji mamy macierze D(E), D(σ1), D(σ2), D(σ3), D(C;+), D(C;-):






Wstęp do reprezentacji równoważnej
[edytuj]Dwie reprezentacje D i D' nazywamy równoważnymi, jeśli istnieje taka macierz A, dla a∈G, dla której macierz A jest taka sama dla wszystkich elementów grupy, zatem przekształcenie między reprezentacjami równoważnymi przestawiamy wedle:

Wstęp do reprezentacji przywiedlnych
[edytuj]Reprezentacja jest reprezentacją przywiedlną, jeśli istnieje ściśle określona macierz S, w której to reprezentacji D(a) tą całą macierz możemy przekształcić do postaci klatkowej za pomocą transformacji równoważnej (16.36), gdzie a∈ G, a jeśli nie da się tego zrobić, to reprezentację nazywamy nieprzywiedlną.

Rozkład reprezentacji na reprezentacje nieprzywiedlne nazywamy sumą prostą tychże reprezentacji i zapisujemy go:

Dla przykładu symetrii molekuły amoniaku określamy przez dwie macierze nieprzywiedlne D1(a) i D2(a), dla każdego elementu grupy G, czyli dla elementów składających się na tą grupę, wiedząc że zachodzi (16.30), (16.31), (16.32), (16.33), (16.34) i macierzy (16.35), zatem na podstawie tego:
| E | σ1 | σ2 | σ3 | C+ | C- | |
| D1 | 
|

|

|

|

|

|
| D2 | 
|

|

|

|

|

|
Właściwości komutacyjne dla reprezentacji nieprzywiedlnej
[edytuj]Jeśli reprezentacja D(a) nieprzywiedlna komutuje z pewną macierzą A, to ta macierz jest prost proporcjonalna do macierzy jednostkowej, co powiemy jako:
![{\displaystyle [A,D(a)]\Rightarrow AD=DA\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e066c8a4a92dd57a1bc2f91d8d570001556b5a2a)
Załóżmy, że macierz A ma wartości własne i jednej wartości własnej odpowiada kilka wektorów własnych, zatem to równanie własne zapisujemy:

Na podstawie własności (16.40) (równanie własne operatora A) i (16.38) (komutacji macierzy A z reprezentacji D(a)) możemy w takim razie napisać obliczenia:
![{\displaystyle A[D(a)u]=D(a)[Au]=D(a)[\lambda u]=\lambda [D(a)u]\Rightarrow A=\lambda E\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f1043146e8b9f30a3b35583a05217b79196234f)
Na podstawie obliczeń przeprowadzonych w punkcie (16.41) możemy napisać własność dla macierzy A, dla której zachodzi A=λE, i która jest pokazana we wspomnianych obliczeniach.
Dowód lematu Schura
[edytuj]Niech mamy dwie reprezentanty D1 i D2, które są reprezentantami nierównoważnymi i nieprzywiedlnymi grupy G, działający oczywiście w przestrzeniach L1 i L2. Operator liniowy odwzorowuje przestrzeń L2 w przestrzeń L1 spełnia własność:

To macierz A jest macierzą zerową. W celu dowodu powyższego lematu, załóżmy, że wymiar przestrzeni L1 jest większy od wymiaru przestrzeni L2, zatem oznaczmy przez M obraz powstały wyniku działania macierzy A na przestrzeń L2, wtedy jest oczywiste, żeby tak zachodziło musi być M∈L1. Zbiór ten M jest przestrzenią niezmienniczą względem operatora D1. Jeśli wykorzystamy ze wzoru (16.42), to możemy napisać tożsamość:

Zatem przestrzeń M pokrywa się w przestrzenią L1, co przeczy twierdzeniu o wymiarach, bo zakładaliśmy, że wymiar przestrzeni L1 jest większy od wymiary przestrzeni L2, zatem dochodzimy do wniosku, że macierz A jest macierzą zerową (A=0).
Pełne przedstawienie twierdzenia o ortogonalności
[edytuj]Weźmy dwie nieprzywiedlne reprezentacje, które będziemy oznaczać wskaźnikami α i β, wybierzmy dla naszych dwóch reprezentacji odpowiednie macierze reprezentujące, tzn. macierze Dαij oraz Dβij, to rozważmy iloczyn skalarny dwóch reprezentacji zapisujemy:

Okazuje się, że tak zdefiniowany iloczyn skalarny na reprezentacjach jest równy:

- gdzie:
- n- to ilość elementów grupy, którą reprezentuje reprezentanta.
- dα -to wymiar przestrzeni grupy, którą reprezentuje dana reprezentanta.
Dowód faktu (16.45) przestawiamy poniżej w tym rozdziale. Załóżmy, że przestrzenie, której wymiar wskazuje reprezentacja ze wskaźnikiem α od reprezentacją ze wskaźnikiem β ma większy wymiar (dα>dβ), zatem na podstawie tego zbudujmy macierz A wedle schematu poniżej i zapisując jednocześnie bardziej szczegółowo wskazując na jego elementy Aim:

Aby udowodnić, czy spełnione jest twierdzenie Schura (16.42) dla dwóch różnych reprezentacji, takich że macierz B jest przekształceniem przestrzeni Lβ w przestrzeń Lα, co udowodnimy, że zachodzi A=0, zatem musimy udowodnić, czy zachodzi ogólnie (16.42):

Na podstawie obliczeń przeprowadzonych w punkcie (16.47) udowodniliśmy, że macierz A spełnia warunek (16.42), zatem macierz A jest równa zero. Jeśli obierzemy macierz, którego elementy macierzy B można zapisać wedle:

Na podstawie definicji elementów macierzy B, czyli według (16.48), że macierz A jest zerowa dla innego α i β, możemy napisać:

Następną częścią dowodu jest założenie, że obie reprezentacje są jednakowe, tzn. α=β, również też zachodzi dowód dla tego przypadku (16.47), które to udowodniliśmy, nie wiedząc jakie wartości przyjmuje α i β, więc gdy obie te liczby są równe, to nie wiemy jakie wartości przyjmuje macierz A, zatem korzystając z twierdzenia udowodnionego w tym module w rozdziale Właściwości komutacyjne dla reprezentacji nieprzywiedlnej, a w nim (16.38), zatem należy powiedzieć, jak udowodniono tam, że macierz A jest macierzą jednostkową pomnożonej przez stałą według (16.41), wtedy macierz:


Elementy macierzy B przestawimy w takiej postaci jak w punkcie (16.48), co na podstawie tego otrzymujemy:

Wtedy do wzoru (16.50) podstawiając do niego otrzymaną tożsamość (16.51), wtedy dostajemy związek:

Ale ponieważ macierz A jest macierzą jednostkową pomnożonej przez stałą λ, wtedy dochodzimy po wstawieniu do niej definicji macierzy Aim poprzez definicję parametru λ określonego w punkcie (16.52), wtedy elementy macierzy A są w postaci:

Elementy macierzy A zapisane wedle wzoru (16.46) przy definicji macierzy B (16.48) i po wykorzystaniu warunku (16.49) dla α nierównego β i wzoru (16.53) dla α=β, wtedy dla dowolnego α i β możemy zapisać wzór łączące oba te dwa przypadki:

Zwykle mamy do czynienia z reprezentacjami unitarnymi, zatem macierz D-1(b) można zastąpić macierzą transponowaną, i która jest sprzężona jeszcze sensie zespolonym. mając wzór (16.54) po wykorzystaniu naszych wniosków wcześniej ostatnio powiedzianych, otrzymujemy (16.45).
Reprezentacje i jego charaktery
[edytuj]Charakter oznaczamy przez symbol χ i jego definicja jest taka, że jest to ślad reprezentacji D(a):

Na podstawie twierdzenia (15.37) charaktery nie zależą od bazy, którego reprezentacje są liczone. Zbiór charakterów opisanych wzorem (16.55), których liczba jest taka sama jak i elementów grupy G, zatem zbiór charakterów tworzy n-wymiarowy wektor, którego to zapis:

Jeśli będziemy rozpatrywać grupę symetrii amoniaku, którego to macierze zapisane są w punkcie Wstęp do reprezentacji przywiedlnych, biorąc reprezentację D1 jako jednowymiarowy wektor, wtedy według tej samej tabelki charakter jest zawsze równy jeden, co zapisujemy:

Następnie biorąc reprezentację dwuwymiarową D2 grupy symetrii amoniaku, wtedy na podstawie tego charaktery dla tej reprezentacji są przestawione wzorami:



Ortogonalna właściwość charakterów
[edytuj]Udowodnimy, że iloczyn skalarny dwóch charakterów charakteryzujące dwie różne reprezentacji przestawiamy:

Iloczyn charakterów zapisanych wedle wzoru (16.61) na podstawie wielkiego twierdzenia ortogonalności na reprezentantach, czyli według wzoru (16.45) jest równy zero, dla α różnego β.
Wyznaczmy normę reprezentacji χα, i wykorzystując wzór (16.45), wtedy mamy wniosek:

Reprezentacje przywiedlne i jego charaktery
[edytuj]Wiadomo, że na podstawie (16.37) reprezentację przywiedlną można przestawić jako sumę prostą reprezentacji nieprzywiedlnych, w której dana reprezentacja może się powtarzać mα, to charakter całej reprezentacji przywiedlnej, po rozkładzie jej na reprezentacje nieprzywiedlne jest równy:

Kryterium nieprzywiedlności reprezentacji
[edytuj]Grupowy kwadrat charakteru danej reprezentacji jest równy modułowi charakterowi całej reprezentacji przywiedlnej, czy według wzorowi określonego wzorem (16.41):

Na podstawie obliczeń przeprowadzonych w punkcie (16.64) kwadrat charakteru reprezentacji przywiedlnej dla określonego "a" jest równy sumie kwadratów współczynników mα, który to wskazuje na ilość powtarzającej się danej reprezentacji nieprzywiedlnej w rozkładzie reprezentacji przywiedlnej na sumą prostą reprezentacji nieprzywiedlnych, pomnożone przez liczbę n. Na podstawie tychże rozważań dochodzimy, że jeśli dana reprezentacja jest przywiedlna, to kwadrat skalarny jej charakteru jest większy niż n.
Charaktery grup przemiennych i jego reprezentacje
[edytuj]Przykładami grup przemiennych są to obroty wokół pewnej osi i translację przestrzenne. Reprezentacje takich grup są reprezentacjami przemiennymi, które ta przemienność jest napisana przez poniższą równość:

Na podstawie twierdzenia udowodnionego w rozdziale Właściwości komutacyjne dla reprezentacji nieprzywiedlnej i z wniosku (16.65) możemy wnioskować, że wszystkie operatory reprezentacji nieprzywiedlnych są operatorami jednostkowymi pomnożonej przez pewną stałą λ, znaczy to, że wszystkie podprzestrzenie niezmiennicze są to przestrzenie jednowymiarowe, jeśli będziemy rozpatrywać reprezentację unitarne, możemy wtedy tą stałą napisać:

Gdy mamy doczynienia z translakcjami, to parametr α jest iloczynem liczby k i translacji x, czyli α=kx, zatem nasz charakter naszej reprezentacji przesunięcia dla reprezentacji nieprzywiedlnych piszemy wedle sposobu:

Dla grup obrotów Cn liczba α jest tak zdefiniowana by była wielokrotnością liczby 2π/n, w takim przypadku parametr α definiujemy wzorem:

Oczywiste jest, że taki wybór parametru α (16.68) zapewnia jednoznaczność dla obrotu o kąt pełny. Ale w obrębie jednej reprezentacji możemy dokonywać obroty będące krotnością l-tą kąta 2π/n, w takim przypadku charakterem m-tym nazywamy liczbę przestawioną:

Jeśli mamy grupę C∞, dopuszczalne są obroty o dowolny kąt, wtedy charakter danej reprezentacji nieprzywiedlnych piszemy przez:

Ostatni wzór jest wzorem do reprezentacji grup obrotów sfery. Wzór (16.69) przechodzi we wzór (16.70), gdy m/n zastąpimy liczbą rzeczywistą.
Definicja iloczynu reprezentacji
[edytuj]Często w fizyce dwa układy opisujemy różnymi wzorami, np. powłoki elektronowe i jadra, które są opisywane różnymi zmiennymi. Łączna grupa symetrii takiego naszego układu jest iloczynem albo kartezjańskim lub prostym, czyli dwóch symetrii związanych z określanymi podukładami jest napisana:

Ten sam zapis stosujemy stosujemy dla każdej reprezentacji naszej rozważanej grupy:

Mnożyć oczywiście możemy niekoniecznie różne reprezentacje tej naszej grupy wedle symetrii danego układu. Charakter reprezentacji (16.72) nazywamy iloczynem ogólnie dwóch charakterów reprezentacji danych dwóch grup: