Elektrodynamika klasyczna/Elementarne właściwości materii w polu magnetycznym
Licencja
|
|---|
|
Autor: Mirosław Makowiecki
Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność. |
Spis treści
|
|---|
Podręcznik: Elektrodynamika klasyczna.
W tym rozdziale zapoznamy się na jakie kryteria dzielimy substancje ze względu na oddziaływania z polem magnetycznym. Wprowadzimy małą teorię jak oddziaływuje pojedynczy dipol z polem magnetycznym zewnętrznym, jaka jest jego energia w tymże polu magnetycznym, i co to jest magnetyzacja ośrodka, która powstaje w wyniku oddziaływania w tymże polu.
Rodzaje magnetyków
[edytuj]Magnetyk jest to substancja, która różnie zachowuje się pod wpływem pola magnetycznego.
Diamagnetyki
[edytuj]Pole magnetyczne wytwarzane przez te substancje jest przeciwne skierowane do kierunku pola zewnętrznego, ale o takim samym kierunku, czyli zatem diamagnetyki osłabiają zewnętrzne pole magnetyczne. Gdy pole magnetyczne zewnętrzne znika, to również pole magnetyczne diamagnetyków wywarzanych na skutek zewnętrznego pola magnetycznego wyniku polaryzacji tego magnetyka też znika.
Paramagnetyki
[edytuj]Pole magnetyczne wytwarzane przez te substancję jest zgodne do kierunku zewnętrznego pola magnetycznego. Te substancje umacniają pole magnetyczne zewnętrzne, którego pole tych magnetyków powstałe jest w wyniku polaryzacji w zewnętrznym polu magnetycznym. Podobnie jak przy diamagnetykach, gdy pole zewnętrze znika, to również pole wytwarzane przez te substancję też znika.
Ferromagnetyki
[edytuj]Są to substancje, które zachowują swoje namagnesowanie nawet wtedy, gdy pole zewnętrzne znika. Teoria jak zachowują się te substancję zależy od historii namagnesowania tychże substancji, i wartości pola indukcji magnetycznej pola zewnętrznego. Jest to pętla histerezy.
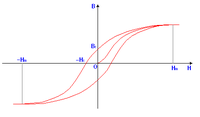
Załóżmy, że ferromagnetyk wcale nie jest namagnesowany, odpowiada to na wykresie punktowi (B,H)=(0,0). Początkowo zwiększajmy pole magnetyczne zewnętrzne, wtedy zwiększa się namagnesowania ferromagnetyka, to można robić do maksymalnego punktu na wykresie. Wtedy można zmniejszyć to pole zewnętrzne aż do zera, wtedy pozostaje namagnesowanie mimo nie istnienia pola zewnętrznego, mimo że ono jest niezerowe. Samo pole ferromagnetyka jest to namagnesowanie resztkowe. Zmieniając pole zewnętrzne, tym razem by było ono przeciwne, i dalej zwiększając to pole w kierunku przeciwnym dochodzi znów do maksymalnej wartości. Następnie można zmniejszyć to pole zewnętrzne aż do wartości zerowej. Dochodzimy znów do namagnesowania resztkowego ferromagnetyka. Znów zmieniając kierunek namagnesowania możemy dojść do maksymalnego namagnesowania maksymalnego i tak dalej.
Pętla histerezy składa się z czterech ćwiartek. Ćwiartka II i IV są ćwiartkami trwałych magnesów.
Momenty sił i same siły działające na dipol magnetyczny
[edytuj]Aby nastąpił obrót ramki wokół osi iksowej, to musi być niezerowy moment siły działający na ramkę. Jedynymi niezerowymi momentami są to momenty działające na prawą i lewą część ramki. Moment siły działający na lewy przewód ramki ma moment siły jest o wartości:

Moment siły działający na lewy przewód ma taką samą wartość jak w punkcie (11.1) i wynosi:

Zwrot i kierunek momentu siły działający na lewy lub prawy przewód ramki jest taki sam, zatem wartość całkowitego momentu siły działający działający na ramkę wynosi:

Przyjmować będziemy, że wartość siły działającą na lewą lub prawą część ramki obliczonej wedle wzoru (8.9) dla naszego przypadku jest:

bo lewy i prawy przewód ramki jest prostopadły do wektora indukcji magnetycznej B pola magnetycznego. A zatem moment siły (11.3), na podstawie siły magnetycznej zdefiniowanej wedle wzoru (11.4), jest równy:

Jeśli przyjmować będziemy, że iloczyn m=SI jest tak zwanym momentem magnetycznym, zatem wyrażenie (11.5) na moment siły działającej na ramkę, korzystając z definicji momentu magnetycznego, jest wyrażony:

Wektor momentu siły o wartości (11.6), znając jego kierunek i zwrot, możemy wyrazić:

W magnetyzmie istnieje coś takiego, że wektor momentu siły stara się by był on ustawiony zgodnie z wektorem indukcji magnetycznej pola magnetycznego. To zjawisko nazywamy paramagnetyzmem.
Policzmy siłę całkowitą działający na dipol elektryczny w niejednorodnym polu magnetycznym na lewą i prawą część ramki dipola magnetycznego, wtedy siła działająca na dipol eletryczny jest sumą sił działająca na część lewą i prawą rozważanego dipola magnetycznego:
![{\displaystyle {\vec {F}}={\vec {F}}_{+}+{\vec {F}}_{-}=I{\vec {l}}\times \left({\vec {B}}_{+}-{\vec {B}}_{-}\right)=I{\vec {l}}\times \delta {\vec {B}}=I{\vec {l}}\times \left[({\vec {a}}\cdot \operatorname {div} ){\vec {B}}\right]=I\left({\vec {a}}\cdot \operatorname {div} \right)\left({\vec {l}}\times {\vec {B}}\right)=I\operatorname {grad} \left[{\vec {a}}\cdot \left({\vec {l}}\times {\vec {B}}\right)\right]=\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f84e928030655e9359f7e7f585db101ed55f5f4)
![{\displaystyle =I\operatorname {grad} \left[{\vec {B}}\left({\vec {a}}\times {\vec {l}}\right)\right]=I\operatorname {div} \left({\vec {B}}\cdot {\vec {S}}\right)=I\left({\vec {S}}\cdot \operatorname {div} \right){\vec {B}}=\left[\left(I{\vec {S}}\right)\cdot \operatorname {div} \right]{\vec {B}}=\left({\vec {\mu }}\cdot \operatorname {div} \right){\vec {B}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6878854ddc02f4397e3fc0f59794d138bc6fbbc1)
Całkowita siła działająca na dipol elektryczny w magnetycznym niejednorodnym polu magnetycznym jest równa:

Jeśli w niejednorodnym polu magnetycznym całkowity moment sił działający na ramkę z prądem jest (11.7) przy wartości siły działającą na lewą i prawą część ramki (11.9), wtedy całkowity moment siły jest równy sumie momentów sił działających na ramkę i na środek masy ramki dla której siła jest napisana wzorem (11.9):

- gdzie:
jest to siła obliczone w (11.9).
Energia dowolnego dipola magnetycznego
[edytuj]Mając wzór na moment siły działający na ramkę z prądem, możemy policzyć jego energię, ale przedtem policzmy jaką wykonuje pracę ramka z prądem przy obrocie jego o kąt 
![{\displaystyle U=\int _{{\pi } \over {2}}^{\alpha }dW=\int _{{\pi } \over {2}}^{\alpha }{\vec {N}}d{\vec {\alpha }}=\int _{{\pi } \over {2}}^{\alpha }\left({\vec {\mu }}\times {\vec {B}}\right)d{\vec {\alpha }}=\int _{{\pi } \over {2}}^{\alpha }\mu B\sin \alpha d\alpha =\mu B[-\cos \alpha ]_{{\pi } \over {2}}^{\alpha }=-\mu B\cos \alpha =-{\vec {\mu }}\cdot {\vec {B}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac0ea89be19a8a9ec000b90f80ea5de07eff1ef6)
Dochodzimy do wniosku, że energia dowolnego dipola na podstawie obliczeń (11.11) jest napisana:

Widzimy, że energia dipola elektrycznego jest równa iloczynowi skalarnemu momentu dipolowego magnetycznego przez wektor indukcji pola magnetycznego.
Orbity atomowe, a wpływ na niego w obecności pola magnetycznego
[edytuj]Elektrony oprócz spinu są wyposażoną w moment pędu, dzięki któremu krążą wokół jądra. Natężeniem prądu elektronów można napisać jako iloraz ładunku elektrycznego posiadającego przez elektron przez okres obiegu elektronu wokół własnej orbity kołowej:

Z definicji prędkości, z którą elektron krąży na obicie kołowej można wyznaczyć z tego wzoru odwrotność okresu, w której elektron okrąży całą orbitę:

Natężenie prądu (11.13) jest równe na podstawie końcowego wzoru na odwrotność okresu (11.14) pomnożonej przez ładunek elektronu:

Z definicji momentu dipolowego, a w nim natężenie prądu jest zdefiniowane wedle (11.15), gdy wiadomo, że S jest kołem o promieniu okręgu r, na którym porusza się elektron, wynika:

Moment dipolowy jest wyrażony wektorowo uwzględniając znak ujemny ładunku elektronu, gdy wiadomo, że jego wartość jest wyrażona wedle wzoru (11.16), a zwrot i kierunek jest zgodny z osią zetową:

W nieobecności pola magnetycznego równanie ruchu elektronu na orbicie kołowej, na której elektron pędzi z prędkością v, jest przedstawiony:

Jeśli w prowadzimy pole magnetyczne jako prostopadłe do płaszczyzny ruchu elektronów na swoich orbitach, wtedy jego równanie ruchu jest w postaci:

Można odejmować równanie (11.19) od równania (11.18) dla tego samego promienia r, na którym torze porusza się elektron, wtedy otrzymujemy tożsamość:

Oznaczmy jako różnice prędkości elektronu na tej samej orbicie, gdy mamy pole magnetyczne prostopadłe do płaszczyzny orbity i bez pola magnetycznego, zatem 


Zmiana prędkość na orbicie oznacza zmianę momentu dipolowego magnetycznego:

Zmiana momentu dipolowego, jeśli skorzystamy z równania (11.17) i policzymy jego zmianę w polu magnetycznym o wspomnianym kierunku przypadku bez pola i potem z udziałem pola, to wtedy podstawiając do niego zmianę prędkości końcowego wyniku (11.22), przestawia się:

Zmiana momentu magnetycznego elektronu krążącego wokół jądra z i bez pola jest zależna od wartości indukcji pola magnetycznego i promienia toru elektronu, który jest okręgiem.
Magnetyzacja substancji magnetycznych pod wpływem pola magnetycznego
[edytuj]Załóżmy, że każda cząsteczka stanowi jakoby ramkę z prądem, w którym płynie pewien prąd, to wtedy jego moment magnetyczny dipolowy wynosi: 

Moment dipolowy ciała może się zmieniać w zależności od natężenia pola magnetycznego panującego w danym ośrodku polaryzacyjnym:

- skalarny współczynnik proporcjonalności γ nazywamy polaryzowalnością magnetyczną .
Całkowity moment magnetyczny jest zależny w ogólności od kierunku prostopadłego i równoległego wyróżnionego w danym ciele magnetycznym i zależy od natężenia pola magnetycznego, który działa na ciało spolaryzowane magnetycznie, który jest zapisany:

- gdzie parametry
i
są to wielkości stałe, lub bardzie ogólnie można zapisać zależność (11.26) w sposób:

Widać w ogólności, że z (11.27), że moment dipolowy ciała nie jest w ogólności równoległy do natężenia pola magnetycznego 
- gdzie
jest pewnym tensorem (macierzą 3x3).
Wyznaczmy jaki jest moment dipolowy w danym nieskończenie małej objętości ciała spolaryzowanego wedle wzoru (11.27):

Załóżmy, że moment dipolowy w objętości ΔV jest równy:

Ogólnie rzecz mówiąc polaryzacja jest to stosunek infinitezymalnego momentu dipolowego znajdującego się w nieskończenie małej objętości dV przez tą właśnie objętość. Wykorzystamy definicję polaryzacji magnetycznej (11.29) i podstawimy do niego wzór (11.28), wtedy dostajemy wyrażenie:

Widzimy, że wektor polaryzacji nie jest w ogólności równoległy do wektora natężenia pola magnetycznego.
Gdy dla danego magnetyka zachodzi 


