Elektrodynamika klasyczna/Rozwinięcia kwadrupolowe

Rozwinięcia kwadrupolowe

---

Licencja

Autor: Mirosław Makowiecki Absolwent UMCS Fizyki Komputerowej Uniwersytetu Marii Curie-Skłodowskiej w Lublinie Email: miroslaw(kropka)makowiecki(małpa)gmail(kropka)pl Dotyczy: książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami. Użytkownika książki, do której należy ta strona, oraz w niej zawartych stron i w nich podstron, a także w nich kolumn, wraz z zawartościami nie zwalnia z odpowiedzialności prawnoautorskiej nieprzeczytanie warunków licencjonowania. Umowa prawna: Creative Commons: uznanie autorstwa, na tych samych warunkach, z możliwością obowiązywania dodatkowych ograniczeń. Autor tej książki dołożył wszelką staranność, aby informacje zawarte w książce były poprawne i najwyższej jakości, jednakże nie udzielana jest żadna gwarancja, czy też rękojma. Autor nie jest odpowiedzialny za wykorzystanie informacji zawarte w książce, nawet jeśli wywołaby jakąś szkodę, straty w zyskach, zastoju w prowadzeniu firmy, przedsiębiorstwa lub spółki bądź utraty informacji, niezależnie czy autor (a nawet Wikibooks) został powiadomiony o możliwości wystąpienie szkód. Informacje zawarte w książce mogą być wykorzystane tylko na własną odpowiedzialność.

---

---

Spis treści
1Dipol elektryczny 2Rozwinięcie multipolowe potencjału skalarnego 3Człon monopolowy i dipolowy w rozwinięciu multipolowym 4Natężenie pola elektrycznego dipola

Będziemy zajmować się multipolami elektrycznymi w celu obliczenia ich natężenia pola elektrycznego w pewnej w odległości od naszego multipola.

Dipol elektryczny

(Rys. 5.1) Rysunek obrazujący pole elektryczne pochodzące od dipola elektrycznego

Potencjał elektryczny w pewnej odległości od dwóch źródeł q i -q dipola elektrycznego, czyli w punkcie O przedstawia się jako suma potencjałów pochodzących od tych ładunków o przeciwnych znakach:

$\varphi ({\vec {r}})={{1} \over {4\pi \epsilon _{0}}}\left({{q} \over {R_{+}}}-{{q} \over {R_{-}}}\right)={{q} \over {4\pi \epsilon _{0}}}\left({{1} \over {R_{+}}}-{{1} \over {R_{-}}}\right)$

(5.1)

Dalszym krokiem jest wyznaczenie odległości R_± za pomocą rysunku obok, przy pomocy odległości pomiędzy tymi omawianymi ładunkami q i -q, oraz przy pomocy odległości łączący środek tego dipola z punktem O, w którym liczymy potencjał elektryczny pochodzący od tego obiektu. Wyznaczmy kwadrat odległości ładunku q od tego ściśle określonego punktu O, w którym liczymy potencjał elektryczny. Jak się przekonamy ona jest zależna od odległości środka dipola elektrycznego od punktu O, jak i odległości w tym obiekcje ładunku q od ładunku przeciwnego -q:

$R_{+}^{2}=r^{2}+\left({{d} \over {2}}\right)^{2}-2r{{d} \over {2}}\cos \phi =r^{2}+{{d^{2}} \over {4}}-rd\cos \phi$

(5.2)

Wyznaczmy kwadrat odległości ładunku -q od tego ściśle określonego punktu O, w którym liczymy potencjał elektryczny. Jak się przekonamy ona jest zależna od odległości środka dipola od punktu O, jak i odległości w dipolu elektrycznym ładunku q od ładunku przeciwnego -q:

$R_{-}^{2}=r^{2}+\left({{d} \over {2}}\right)^{2}-2r{{d} \over {2}}\cos(\pi -\phi )=r^{2}+{{d^{2}} \over {4}}+rd\cos \phi$

(5.3)

Co do wzorów (5.2) (ona przedstawia odległość ładunku q od punktu O) i (5.3) (ona przedstawia odległość ładunku -q od punktu O), co można zapisać te dwa wzory równoważnie obejmującą oba te przypadki, za pomocą znaku plus minus, czyli znaku ±, wedle:

$R_{\pm }^{2}=r^{2}+{{d^{2}} \over {4}}\mp rd\cos \phi$

(5.4)

Policzmy odwrotności wielkości R_± zapisanej ogólnie wedle wzoru (5.4), które są z osobna odległościami ładunku q i -q od rozważanego punktu O, mamy stąd wniosek:

${{1} \over {R_{\pm }}}={{1} \over {\left(r^{2}+{{d^{2}} \over {4}}\mp rd\cos \phi \right)^{{1} \over {2}}}}\simeq {{1} \over {r\left(1\mp {{d\cos \phi } \over {r}}\right)^{{1} \over {2}}}}\simeq {{1} \over {r}}\left(1\pm {{d} \over {2r}}\cos \phi \right)$

(5.5)

Policzmy wyrażenie, które mówi nam jaka jest wartość potencjału elektrycznego w naszym omawianym punkcie, czyli według wzoru (5.1), korzystając ze wzoru ogólnego (5.5), mówiący jakie są odległości ładunku q lub -q od naszego punktu, zatem policzmy najpierw ostatni czynnik tej tożsamości:

${{1} \over {R_{+}}}-{{1} \over {R_{-}}}={{1} \over {r}}\left(1+{{d} \over {2r}}\cos \phi \right)-{{1} \over {r}}\left(1-{{d} \over {2r}}\cos \phi \right)={{d} \over {r^{2}}}\cos \phi$

(5.6)

By potem napisać nasz potencjał (5.1) wedle wzoru (5.6), przedstawiający różnicę odwrotności ładunków q i -q od punktu O, której ten potencjał jest równy wyrażeniu:

$\varphi ({\vec {r}})={{q} \over {4\pi \epsilon _{0}}}{{d} \over {r^{2}}}\cos \phi ={{qd\cos \phi } \over {4\pi \epsilon _{0}r^{2}}}$

(5.7)

Potencjał elektryczny pochodzący od dipola będziemy liczyli w pewnej odległości od niego, korzystając z definicji momentu dipolowego o wartości:

$p=qd\;$

(5.8)

• gdzie d jest to odległość łącząca ładunki q (ładunek dodatni) i -q (ładunek ujemny) w dipolu elektrycznym.

jeśli moment dipolowy przedstawić jako wektor, to jego kierunek pokrywa się z prostą łączącą oba te ładunki, a zwrot jest od ładunku ujemnego do dodatniego. Potencjał skalarny (5.7) jest taki, że wykorzystując wzór na wartość momentu dipolowego (5.8), wtedy wyraża się on:

$\varphi ({\vec {r}})={{p\cos \phi } \over {4\pi \epsilon _{0}r^{2}}}$

(5.9)

Jest to wzór na potencjał skalarny dipola, który jest funkcją jego momentu dipolowego, odległości środka dipola od punktu, w którym ten potencjał skalarny istnieje, a także od kąta pomiędzy wektorem łączący dwa skrajne ładunki w dipolu elektrycznym, a wektorem łączący środek dipola elektrycznego z punktem, w którym liczymy nasz wspomniany potencjał.

Rozwinięcie multipolowe potencjału skalarnego

(Rys. 5.2) Rozwinięcie multipolowe dla pola elektrycznego

Mamy sobie pewien rozkład ładunków i będziemy liczyli potencjał skalarny w pewnym punkcie, którego wektor wodzący jest ${\vec {r}}\;$ względem pewnego punktu. Również znamy wektory wodzące ${\vec {r}}^{'}\;$ infinitezymalnych objętości. Na podstawie tych naszych dysput możemy wyznaczyć odległość infinitezymalnego ładunków, który ten ładunek znajduje się w infinitezymalnej objętości, od punktu O. Mając już obliczony odległość R, które możemy wykorzystać do liczenia potencjału skalarnego według wzoru napisanego w punkcie (3.19). Ta nasza wspomniana odległość R, którą będziemy wyznaczać wedle rysunku obok, jest napisana:

$R^{2}=r^{2}+(r^{'})^{2}-2rr^{'}\cos \phi =r^{2}\left[1+\left({{r^{'}} \over {r}}\right)^{2}-2\left({{r^{'}} \over {r}}\right)\cos \phi \right]$

(5.10)

Widzimy, że ona jest funkcją r i odległości r^', które są wyznaczane względem pewnego punktu, który nazwiemy punktem bazowym. Obierzmy odległość R (5.10) poprzez parametr ε, który jest zdefiniowany w wspomnianym wzorze w sposób równoważny wedle:

$R=r{\sqrt {1+\epsilon }}$

(5.11)

• gdzie ten nasz wspomniany parametr ε jest opisany wzorem:

$\epsilon =\left({{r^{'}} \over {r}}\right)\left({{r^{'}} \over {r}}-2\cos \phi \right)$

(5.12)

Odwrotność promienia R (5.11) przy definicji parametru ε (5.12) możemy wyrazić jako:

${{1} \over {R}}={{1} \over {r}}\left(1+\epsilon \right)^{-{{1} \over {2}}}\simeq {{1} \over {r}}\left(1-{{1} \over {2}}\epsilon +{{3} \over {8}}\epsilon ^{2}-{{5} \over {16}}\epsilon ^{3}+....\right)$

(5.13)

Wykorzystajmy definicję parametru ε, który jest opisana według wzoru (5.12) do wzoru, który jest odwrotnością R (5.13), mamy:

${{1} \over {R}}={{1} \over {r}}{\Bigg [}1-{{1} \over {2}}\left({{r^{'}} \over {r}}\right)\left({{r^{'}} \over {r}}-2\cos \phi \right)+{{3} \over {8}}\left({{r^{'}} \over {r}}\right)^{2}\left({{r^{'}} \over {r}}-2\cos \phi \right)^{2}-{{5} \over {16}}\left({{r^{'}} \over {r}}\right)^{3}\left({{r^{'}} \over {r}}-2\cos \phi \right)^{3}{\Bigg ]}=$
$={{1} \over {r}}{\Bigg [}1-{{1} \over {2}}\left({{r^{'}} \over {r}}\right)^{2}+{{r^{'}} \over {r}}\cos \phi +{{3} \over {8}}\left({{r^{'}} \over {r}}\right)^{2}\left(\left({{r^{'}} \over {r}}\right)^{2}+4\cos ^{2}\phi -4{{r^{'}} \over {r}}\cos \phi \right)+\;$
$-{{5} \over {16}}\left({{r^{'}} \over {r}}\right)^{3}\left(\left({{r^{'}} \over {r}}\right)^{3}+8\cos ^{3}\phi -6{{(r^{'})^{2}} \over {r^{2}}}cos\phi +12{{r^{'}} \over {r}}\cos ^{2}\phi \right){\Bigg ]}$

(5.14)

We wzorze (5.14) w nawiasie grupujemy kolejne wyrazy względem potęg ${{r^{'}} \over {r}}$, a zatem do dzieła.

${{1} \over {R}}={{1} \over {r}}\left[1+{{r^{'}} \over {r}}\cos \phi +\left({{r^{'}} \over {r}}\right)^{2}{{(3\cos ^{2}\phi -1)} \over {2}}+\left({{r^{'}} \over {r}}\right)^{3}{{\left(5\cos ^{2}\phi ^{3}-3\cos \phi \right)} \over {2}}+...\right]$

(5.15)

Rozszerzając powyższy wzór (5.15), który można tak rozszerzyć na wszystkie wyrazy zależne od współczynnika n dla P_n(x), które są wielomianami Legendre'a.

${{1} \over {R}}={{1} \over {r}}\sum _{n=0}^{\infty }\left({{r^{'}} \over {r}}\right)^{n}P_{n}(\cos \phi )$

(5.16)

Całkowity potencjał elektryczny (3.19) i korzystając przy tym z (5.16) na odwrotność promienia R, wyrażona jest w postaci całki po ładunkach należących do tego rozkładu według wzoru:

$\varphi ({\vec {r}})={{1} \over {4\pi \epsilon _{0}}}\sum _{n=0}^{\infty }{{1} \over {r^{n+1}}}\int (r^{'})^{n}P_{n}(\cos \phi )\rho ({\vec {r}}^{'})dV^{'}$

(5.17)

lub w postaci jawnej biorąc ze wzoru (5.17) trzy pierwsze wyrazy, a pozostałe oznaczając wielokropkami:

$\varphi ({\vec {r}})=\;$
$={{1} \over {4\pi \epsilon _{0}}}\left[{{1} \over {r}}\int \rho ({\vec {r}}^{'})dV^{'}+{{1} \over {r^{2}}}\int r^{'}\cos \phi \rho ({\vec {r}}^{'})dV^{'}+{{1} \over {r^{3}}}\int (r^{'})^{2}\left({{3} \over {2}}\cos ^{2}\phi dV^{'}-{{1} \over {2}}\right)\rho ({\vec {r^{'}}})dV^{'}+....\right]$

(5.18)

Patrząc na powyższe rozwinięcie mamy dla n=0 człon monopolowy, dla n=1 człon dipolowy i ostatecznie dla b=3 człon kwadrupolowy. Potencjał elektryczny można liczyć w prowadzając pewne poprawki jako multipole.

Człon monopolowy i dipolowy w rozwinięciu multipolowym

Człon monopolowy występujący we wzorze (5.18) jest dokładnie taki sam jak w równaniu (3.20) na potencjał skalarny wytwarzanej przez rozciągły rozkład ładunków nieskończenie małych z pewnymi gęstościami objętościowymi ładunków elektrycznych.

$\varphi _{0}({\vec {r}})={{1} \over {4\pi \epsilon _{0}}}\int {{\rho ({\vec {r}}^{'})} \over {r}}dV^{'}$

(5.19)

A człon dipolowy występujący również w tym samym równaniu jest zależny od gęstości objętościowej ładunków w danej badanej objętości i od kąta φ wedle kulistego układu współrzędnych, potencjał elektryczny pochodzący od dipoli jest wyrażony:

$\varphi _{1}({\vec {r}})={{1} \over {4\pi \epsilon _{0}}}{{1} \over {r^{2}}}\int r^{'}\cos \phi \rho ({\vec {r^{'}}})dV^{'}$

(5.20)

Określmy jako: ${\hat {r}}{\vec {r}}^{'}=r^{'}\cos \phi$,

• gdzie:${\hat {r}}$ jest wektorem równoległym i jednostkowym do wektora wodzącego ${\vec {r}}\;$, w którym ta ostatnia łączy punkt O z pewnym punktem, którego ma początek wspomniany wektor, i na końcu tego wektora będziemy liczymy potencjał elektryczny skalarny pola wytwarzanego przez pewien rozkład ładunków, i która z ${\vec {r}}^{'}$ tworzy pewien kąt.

Dochodzimy do wniosku, że wyrażenie (5.20) możemy napisać:

$\varphi _{1}({\vec {r}})={{1} \over {4\pi \epsilon _{0}}}{{1} \over {r^{2}}}\int {\hat {r}}{\vec {r}}^{'}\rho ({\vec {r^{'}}})dV^{'}\Rightarrow \varphi _{1}({\vec {r}})={{1} \over {4\pi \epsilon _{0}}}{{1} \over {r^{2}}}{\hat {r}}\int {\vec {r}}^{'}\rho ({\vec {r^{'}}})dV^{'}$

(5.21)

Jeśli zdefiniujemy, że wektor momentu dipolowego dielektryka jako całkę objętościową z iloczynu gęstości objętościowej ładunków jakie panują w danym punkcie przez położenie tego punktu określonej przez wektor ${\vec {r}}^{'}\;$:

${\vec {p}}=\int {\vec {r}}^{'}\rho ({\vec {r}}^{'})dV^{'}$

(5.22)

Po wykorzystaniu wzoru na moment dipolowy zdefiniowanej w linijce (5.22) do wyrażenia na potencjał skalary pochodząca od pewnego rozciągłego dipola elektrycznego (5.21), wtedy:

$\varphi _{1}({\vec {r}})={{1} \over {4\pi \epsilon _{0}}}{{{\vec {p}}\cdot {\hat {r}}} \over {r^{2}}}$

(5.23)

W postaci dyskretnej, gdy ładunki nie są infinitezymalnie małe, ale mają wartości skończone i rozłożone są jakoś w przestrzeni, wtedy moment dipolowy takiego rozkładu ładunków jest napisany:

${\vec {p}}=\sum _{n=0}^{n}q_{n}r_{n}^{'}$

(5.24)

Całkowity ładunek indukowany w dielektryku wynosi zero. A zatem ładunkowi ujemnemu odpowiada ładunek dodatni o takim samym co do wartości ładunku. Jeśli mamy:

${\vec {p}}=q{\vec {r}}_{+}^{'}-q{\vec {r}}_{-}^{'}=q({\vec {r}}_{+}^{'}-{\vec {r}}_{-}^{'})=q{\vec {d}}$

(5.25)

To dochodzimy do wniosku, że definicja momentu dipolowego dla układu w postaci ciągłej (5.22) jak i dla układów dyskretnych dipoli (5.24) jest poprawną definicją.

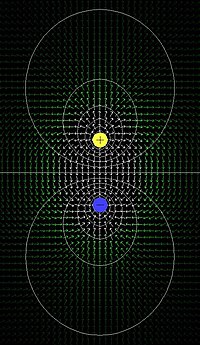
Natężenie pola elektrycznego dipola

(Rys. 5.3) Poli linii natężenia pola elektrycznego dipola elektrycznego

Dotąd zajmowaliśmy jedynie potencjałami elektrycznymi jako wielkościami skalarnymi. Teraz będziemy zajmować się wyznaczaniem pola wektorowego w postaci natężenia pola elektrycznego, co tutaj będziemy wyznaczali tą wielkość we współrzędnych kulistych. Potencjał elektryczny dipola jest określony według wzoru (5.9), i wtedy aby otrzymać pole wektorowe natężenia pola elektrycznego należy policzyć gradient potencjału elektrycznego wedle wzoru (3.5), korzystać będziemy z definicji tego gradientu we współrzędnych sferycznych:

$\operatorname {grad} =\left({{\partial } \over {\partial r}},{{1} \over {r\sin \phi }}{{\partial } \over {\partial \theta }},{{1} \over {r}}{{\partial } \over {\partial \phi }}\right)\;$

Wtedy poszczególne współrzędne w układzie kulistym natężenia pola elektrycznego wyrażamy, korzystając z definicji gradientu, który ostatnio wspominaliśmy, są wyrażone przez:

${\begin{cases}E_{r}=-{{\partial \varphi _{1}({\vec {r}})} \over {\partial r}}={{2p\cos \phi } \over {4\pi \epsilon _{0}r^{3}}}\\E_{\theta }=-{{1} \over {r\sin \phi }}{{\partial \varphi _{1}({\vec {r}})} \over {\partial \theta }}=0\\E_{\phi }=-{{1} \over {r}}{{\partial \varphi _{1}({\vec {r}})} \over {\partial \phi }}={{p\sin \phi } \over {4\pi \epsilon _{0}r^{3}}}\end{cases}}$

(5.26)

Wektor natężenia pola elektrycznego wytwarzane przez dipol elektryczny przedstawia się:

${\vec {E}}={{p} \over {4\pi \epsilon _{0}r^{3}}}\left(2\cos \phi {\hat {e}}_{r}+\sin \phi {\hat {e}}_{\phi }\right)$

(5.27)

Jest to natężenie pola elektrycznego pochodzące od dipola elektrycznego w układzie kulistym i jest funkcją odległości środka dipola z punktem, w którym liczymy tą wielkość, która to (5.27) wyznacza wielkość wektorową zależną od wersorów pochodzących od układu kulistego w tym punkcie.